Question

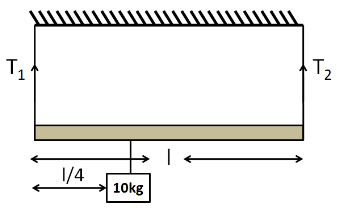
What will $ {T_1} $ and $ {T_2} $ be in the given diagram? Mass of rod $ 20kg $ .

(A) $ 175N $ , $ 125N $
(B) $ 125N $ , $ 175N $
(C) $ 150N $ , $ 150N $
(D) $ 300N $ , $ zero $

Answer 1

Hint: For solving this question, we need to consider the free body diagram of the given rod. Then, applying the conditions of the vertical and rotational equilibrium about any point, we will have two linear equations in the form of the unknown tensions $ {T_1} $ and $ {T_2} $ . On solving the two equations we will get the respective values of the tensions.

Complete step-by-step solution
We know that the weight of a body acts on its centre of gravity. We also know that the centre of gravity of a uniform rod lies at its centre. So the weight of the given rod will act on its centre, as shown in the below free body diagram of the rod.

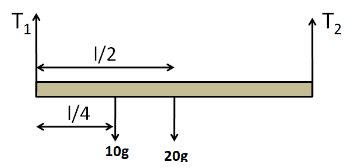
Considering the vertical equilibrium of the rod, we have
 $ {T_1} + {T_2} - 10g - 20g = 0 $
 $ {T_1} + {T_2} = 30g $ ............(1)
Now, we consider the rotational equilibrium of the rod at the leftmost end. Rotational equilibrium at a point means the net torque at that point will be equal to zero. So we have
 $ {T_2}\left( l \right) - 20g\left( {l/2} \right) - 10g\left( {l/4} \right) = 0 $
 $ \Rightarrow {T_2}\left( l \right) = 20g\left( {l/2} \right) + 10g\left( {l/4} \right) $
Dividing both sides by $ l $ we get
 $ {T_2} = 10g + 2.5g $
 $ \Rightarrow {T_2} = 12.5g $ ............(2)
Substituting (2) in (1) we get
 $ {T_1} + 12.5g = 30g $
 $ \Rightarrow {T_1} = 17.5g $ ............(3)
Substituting $ g = 10m/{s^2} $ in (2) and (3) we get
 $ {T_1} = 175N $
And
 $ {T_2} = 125N $
Thus, the values of the tensions $ {T_1} $ and $ {T_2} $ are $ 175N $ and $ 125N $ respectively.
Hence, the correct answer is option A.

Note
For the rotational equilibrium of the rod, we can equal the net torque about any point on the rod equal to zero. But preference should be given to the point such that the value of the torque due to at least one unknown force becomes equal to zero. Using this trick we can get the answer more quickly.