Question

What is the surface area formula of a 3-dimensional rectangle?

Answer 1

Hint: We surface area is always calculated for 2-dimensional figures, and so we can visualize a cuboid as a combination of rectangles, and add these areas to get the total surface area of a 3-dimensional rectangle.

Complete step by step solution:
We know that a rectangle is a 2-dimensional figure. We have shown a rectangle of length l and breadth b in the following figure,

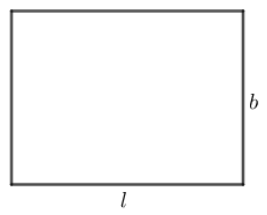
We know that in a rectangle, the opposite sides are equal and parallel. Also, we are aware that each one of the angles of a rectangle is a right angle.
To convert this 2-dimensional shape into 3-dimensional, let us put similar rectangles on the top of this one, in similar orientation. We will see that we get a heap of rectangles, shaped like a box. This shape is called a cuboid. We have shown a cuboid of length l, breadth b and height h in the figure below,

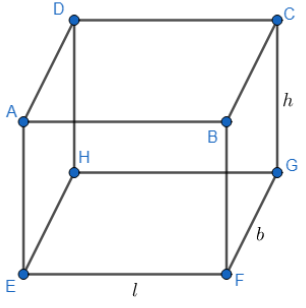
Here, in this figure, we can see that ABCDEFGH is a cuboid. We need to find the surface area of this cuboid. This surface area will be equal to the sum of individual surface areas of each rectangle.
We also know that the opposite faces of a cuboid have the same dimensions, and so the same area.
So, we can write,
Area of face ABCD = Area of face EFGH
Area of face BCGF = Area of face ADHE
Area of face ABFE = Area of face DCGH
Thus, from the figure, we can write,
Surface area of cuboid ABCDEFGH
= $2\times $Surface area of ABCD + $2\times $Surface area of BCGF + $2\times $Surface area of ABFE
Thus, the surface area S,
$S=2\left( lb \right)+2\left( bh \right)+2\left( lh \right)$
Thus, the surface area of the 3-dimensional rectangle is $S=2\left( lb+bh+lh \right)$.

Note: We must remember that as all squares are rectangles, but not all rectangles are square, similarly, all cubes are cuboids, but all cuboids are not cubes. Cuboids are also sometimes referred to as closed boxes.