Question

Suppose you are shooting an arrow from the top of a building at a height of $6{\text{m}}$ to a target on the ground at an angle of depression of $60^\circ $. What is the distance between you and the object?

Answer 1

Hint: Here we just need to fist redraw the given statement in the form of the figure and then we can use the trigonometric function in order to find the distance between you and the object. Here we must know that the angle of depression is the angle between the horizontal line of sight of an object and the object which he is seeing.

Complete Step by Step Solution:
Here we are given that we need to find the distance between you and the object and it is told that you are shooting an arrow from the top of a building at a height of $6{\text{m}}$ to a target on the ground at an angle of depression of$60^\circ $.
So we know that the angle of depression is the angle between the horizontal line of sight of an object and the object which he is seeing.
So let us draw it as a figure and get:

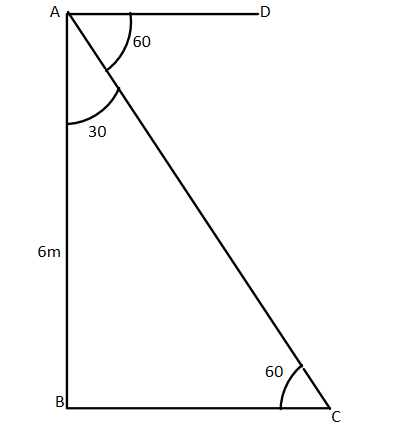
Let ABC be the right angled triangle and here we are given according to the question that angle of depression is $60^\circ $
So we can say that
$\angle CAD = 60^\circ $
Now we can see that by the figure:
$\angle ACB = 60^\circ $ as these both are the interior alternate angles.
Now we can say that:
$
  \sin \angle CAD = \dfrac{{AB}}{{AC}} \\
  \sin 60^\circ = \dfrac{6}{{AC}} \\
  \dfrac{{\sqrt 3 }}{2} = \dfrac{6}{{AC}} \\
  AC = \dfrac{{12}}{{\sqrt 3 }} = \dfrac{{12\sqrt 3 }}{3} = 4\sqrt 3 \\
 $

Hence we get the distance to be $4\sqrt 3 $ between you and the object.

Note:
Here in these types of problems the diagram plays a very vital role as if the figure drawn is not correct the whole problem will go wrong. Hence one must draw the figure properly.