Question

Sum of the length, width and depth of a cuboid is “s” and its diagonal is “d”. Find its surface area.
(a) ${{s}^{2}}-{{d}^{2}}$
(b) ${{s}^{2}}+{{d}^{2}}$
(c) ${{s}^{2}}\times {{d}^{2}}$
(d) None of these

Answer 1

Hint: Let us assume that length, width and depth of a cuboid as l, b and h respectively. The sum of these sides of the cuboid is given as “s” so equating the addition of l, b and h to s. And length of diagonal of the cuboid is given as d and we know that the length of diagonal of a cuboid is equal to $\sqrt{{{l}^{2}}+{{b}^{2}}+{{h}^{2}}}$. Now, rearranging this relation between d and s with l, b and h we get the required relation.

Complete step by step answer:
We have given a cuboid with sum of its length, width and depth as “s” and length of its diagonal as “d”.
Let us assume that length, width and height of a cuboid as l, b and h respectively.
In the below figure, we have shown a cuboid with length, width and depth as l, b and h respectively and also the diagonal of the cuboid.

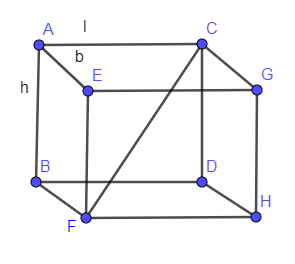
In the above figure, CF is the diagonal of the cuboid. And we have shown AC, AE and AB as the length, width and depth of the cuboid.
We know the formula for the length of the diagonal of the cuboid which is equal to:
$\sqrt{{{l}^{2}}+{{b}^{2}}+{{h}^{2}}}$
It is given that length of the diagonal is equal to “d” so equating the above expression to “d” we get,
$\sqrt{{{l}^{2}}+{{b}^{2}}+{{h}^{2}}}=d$
Squaring on both the sides we get,
${{l}^{2}}+{{b}^{2}}+{{h}^{2}}={{d}^{2}}$…….. Eq. (1)
Sum of the length, width and height is given as “s” then addition of l, b and h we get,
$l+b+h$
Equating the above expression to s we get,
$l+b+h=s$
Squaring on both the sides we get,
$\begin{align}
  & {{\left( l+b+h \right)}^{2}}={{s}^{2}} \\
 & \Rightarrow {{l}^{2}}+{{b}^{2}}+{{h}^{2}}+2\left( lb+bh+hl \right)={{s}^{2}} \\
\end{align}$
Using eq. (1) in the above equation we get,
$\begin{align}
  & {{d}^{2}}+2\left( lb+bh+hl \right)={{s}^{2}} \\
 & \Rightarrow 2\left( lb+bh+hl \right)={{s}^{2}}-{{d}^{2}}..........Eq.(2) \\
\end{align}$
And we know that, surface area of the cuboid is equal to:
$2\left( lb+bh+hl \right)$
Hence, the surface area of the cuboid from eq. (2) is equal to ${{s}^{2}}-{{d}^{2}}$.

So, the correct answer is “Option A”.

Note: The mistake that you could make in this problem is to forget to write the 2 in the surface area formula i.e. $2\left( lb+bh+hl \right)$. Generally, in the haste of solving the problem in examination, students forget to double this expression $lb+bh+hl$. The other common mistake is that, instead of writing the length of the diagonal as $\sqrt{{{l}^{2}}+{{b}^{2}}+{{h}^{2}}}$ you might write this formula of the length of diagonal as $\dfrac{1}{3}\sqrt{{{l}^{2}}+{{b}^{2}}+{{h}^{2}}}$.