Question

Sum of the areas of two squares is $468{{m}^{2}}$. If the difference of their perimeters is 24m, formulate the quadratic equation to find the sides of the two squares.

Answer 1

Hint: Assume that the length of sides of both the squares is ‘x’ and ‘y’. Use the fact that if the length of the side of the square is ‘a’, then its perimeter is 4a and the area is ${{a}^{2}}$. Write an equation relating the length of sides of both two squares. Simplify them to get the quadratic equation relating the length of sides of both the squares.

Complete step-by-step answer:
We have data regarding the sum of areas of two squares and the difference of their perimeters. We have to formulate a quadratic equation to find the sides of both the squares.
Let’s assume that there are two squares ABCD and PQRS, with sides of length x and y, as shown in the figure.

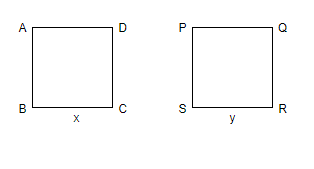
We know that if the length of the side of the square is ‘a’, then its perimeter is 4a and the area is ${{a}^{2}}$.
Thus, the area of square ABCD is ${{x}^{2}}$ and its perimeter is 4x.
Similarly, the area of square PQRS is ${{y}^{2}}$ and its perimeter is 4y.
We know that the sum of areas of both the squares is $468{{m}^{2}}$. Thus, we have ${{x}^{2}}+{{y}^{2}}=468.....\left( 1 \right)$.
We know that the difference of perimeters of both the squares is 24m. Thus, we have $4x-4y=24$. Rearranging the terms of the previous equation, we have $x-y=\dfrac{24}{4}=6.....\left( 2 \right)$
We can rewrite the above equation as $x=y+6$.
Squaring the above equation on both sides, we have ${{x}^{2}}={{\left( y+6 \right)}^{2}}={{y}^{2}}+12y+36.....\left( 3 \right)$.
Substituting equation (3) in equation (1), we have ${{y}^{2}}+12y+36+{{y}^{2}}=468$.
Simplifying the above equation, we have $2{{y}^{2}}+12y+=468-36=432\Rightarrow {{y}^{2}}+6y=216$ .
Hence, the quadratic equation which can be used to find the side of squares is ${{y}^{2}}+6y-216=0$.

Note: We can factorize this equation to find the value of y and then substitute it in the equation relating ‘x’ and ‘y’ to calculate the value of ‘x’. We can then verify the calculated values of ‘x’ and ‘y’ by substituting the values in the equation and then checking if they satisfy the equation or not.