
What should be subtracted from the polynomial \[5{x^4} - 15{x^3} + 2{x^2}\] so that \[5{x^3} - 1\] becomes its factor?
Answer
568.5k+ views
Hint: Here we will use the concept of factor of a polynomial. If a number is a factor of a polynomial, this means that the polynomial is exactly divisible by the number, and leaves remainder 0 when divided by it. Therefore, if the remainder is subtracted from the dividend, the result will be exactly divisible by the divisor.
Complete step-by-step answer:
We know that if \[x\] is a factor of a polynomial \[p\left( x \right)\], then \[p\left( x \right)\] is exactly divisible by \[x\].
This means that when \[p\left( x \right)\] is divided by \[x\], the remainder should be equal to 0.
Now, we know that the division algorithm states that if \[p\left( x \right)\] and \[g\left( x \right)\] are two polynomials where \[g\left( x \right) \ne 0\], then there are two polynomials \[q\left( x \right)\] and \[r\left( x \right)\] such that \[p\left( x \right) = q\left( x \right) \times g\left( x \right) + r\left( x \right)\]. In other words, \[{\rm{Dividend}} = {\rm{Quotient}} \times {\rm{Divisor}} + {\rm{Remainder}}\].
Rewriting the division algorithm, we get
\[\begin{array}{l} \Rightarrow p\left( x \right) - r\left( x \right) = q\left( x \right) \times g\left( x \right)\\ \Rightarrow \dfrac{{p\left( x \right) - r\left( x \right)}}{{g\left( x \right)}} = q\left( x \right)\end{array}\]
This means that if the remainder is subtracted from the dividend, then the resulting polynomial will be exactly divisible by the divisor.
Therefore, we need to use a long division method to divide \[5{x^4} - 15{x^3} + 2{x^2}\] by \[5{x^3} - 1\].
The remainder obtained will be the polynomial/number that should be subtracted from the polynomial \[5{x^4} - 15{x^3} + 2{x^2}\] so that \[5{x^3} - 1\] becomes its factor.
Now, let us use a long division method to divide \[5{x^4} - 15{x^3} + 2{x^2}\] by \[5{x^3} - 1\].
Therefore, we get
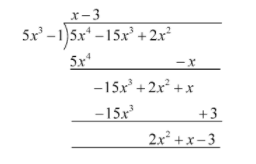
Therefore, \[2{x^2} + x - 3\] should be subtracted from \[5{x^4} - 15{x^3} + 2{x^2}\] so that \[5{x^3} - 1\] becomes its factor.
We can also verify our answer by subtracting \[2{x^2} + x - 3\] from \[5{x^4} - 15{x^3} + 2{x^2}\].
Subtracting \[2{x^2} + x - 3\] from \[5{x^4} - 15{x^3} + 2{x^2}\], we get
\[\begin{array}{l} \Rightarrow 5{x^4} - 15{x^3} + 2{x^2} - \left( {2{x^2} + x - 3} \right) = 5{x^4} - 15{x^3} + 2{x^2} - 2{x^2} - x + 3\\ \Rightarrow 5{x^4} - 15{x^3} + 2{x^2} - \left( {2{x^2} + x - 3} \right) = 5{x^4} - 15{x^3} - x + 3\end{array}\]
Factorising the right hand side of the equation, we get
\[\begin{array}{l} \Rightarrow 5{x^4} - 15{x^3} + 2{x^2} - \left( {2{x^2} + x - 3} \right) = 5{x^3}\left( {x - 3} \right) - 1\left( {x - 3} \right)\\ \Rightarrow 5{x^4} - 15{x^3} + 2{x^2} - \left( {2{x^2} + x - 3} \right) = \left( {5{x^3} - 1} \right)\left( {x - 3} \right)\end{array}\]
Therefore, we can observe that when \[2{x^2} + x - 3\] is subtracted from \[5{x^4} - 15{x^3} + 2{x^2}\], \[5{x^3} - 1\] becomes a factor of \[5{x^4} - 15{x^3} + 2{x^2}\].
Hence, we have verified the answer.
Note: We need to be careful while doing the long division. When multiplying \[5{x^3} - 1\] by \[x\], the product of \[ - 1\] and \[x\] is \[ - x\]. Since the dividend has no term from which \[ - x\] can be subtracted, we have placed the term at the end of the dividend. Similarly, we have placed 3 at the end in the next step.
Complete step-by-step answer:
We know that if \[x\] is a factor of a polynomial \[p\left( x \right)\], then \[p\left( x \right)\] is exactly divisible by \[x\].
This means that when \[p\left( x \right)\] is divided by \[x\], the remainder should be equal to 0.
Now, we know that the division algorithm states that if \[p\left( x \right)\] and \[g\left( x \right)\] are two polynomials where \[g\left( x \right) \ne 0\], then there are two polynomials \[q\left( x \right)\] and \[r\left( x \right)\] such that \[p\left( x \right) = q\left( x \right) \times g\left( x \right) + r\left( x \right)\]. In other words, \[{\rm{Dividend}} = {\rm{Quotient}} \times {\rm{Divisor}} + {\rm{Remainder}}\].
Rewriting the division algorithm, we get
\[\begin{array}{l} \Rightarrow p\left( x \right) - r\left( x \right) = q\left( x \right) \times g\left( x \right)\\ \Rightarrow \dfrac{{p\left( x \right) - r\left( x \right)}}{{g\left( x \right)}} = q\left( x \right)\end{array}\]
This means that if the remainder is subtracted from the dividend, then the resulting polynomial will be exactly divisible by the divisor.
Therefore, we need to use a long division method to divide \[5{x^4} - 15{x^3} + 2{x^2}\] by \[5{x^3} - 1\].
The remainder obtained will be the polynomial/number that should be subtracted from the polynomial \[5{x^4} - 15{x^3} + 2{x^2}\] so that \[5{x^3} - 1\] becomes its factor.
Now, let us use a long division method to divide \[5{x^4} - 15{x^3} + 2{x^2}\] by \[5{x^3} - 1\].
Therefore, we get
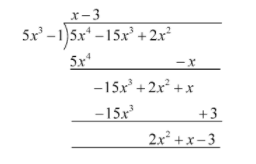
Therefore, \[2{x^2} + x - 3\] should be subtracted from \[5{x^4} - 15{x^3} + 2{x^2}\] so that \[5{x^3} - 1\] becomes its factor.
We can also verify our answer by subtracting \[2{x^2} + x - 3\] from \[5{x^4} - 15{x^3} + 2{x^2}\].
Subtracting \[2{x^2} + x - 3\] from \[5{x^4} - 15{x^3} + 2{x^2}\], we get
\[\begin{array}{l} \Rightarrow 5{x^4} - 15{x^3} + 2{x^2} - \left( {2{x^2} + x - 3} \right) = 5{x^4} - 15{x^3} + 2{x^2} - 2{x^2} - x + 3\\ \Rightarrow 5{x^4} - 15{x^3} + 2{x^2} - \left( {2{x^2} + x - 3} \right) = 5{x^4} - 15{x^3} - x + 3\end{array}\]
Factorising the right hand side of the equation, we get
\[\begin{array}{l} \Rightarrow 5{x^4} - 15{x^3} + 2{x^2} - \left( {2{x^2} + x - 3} \right) = 5{x^3}\left( {x - 3} \right) - 1\left( {x - 3} \right)\\ \Rightarrow 5{x^4} - 15{x^3} + 2{x^2} - \left( {2{x^2} + x - 3} \right) = \left( {5{x^3} - 1} \right)\left( {x - 3} \right)\end{array}\]
Therefore, we can observe that when \[2{x^2} + x - 3\] is subtracted from \[5{x^4} - 15{x^3} + 2{x^2}\], \[5{x^3} - 1\] becomes a factor of \[5{x^4} - 15{x^3} + 2{x^2}\].
Hence, we have verified the answer.
Note: We need to be careful while doing the long division. When multiplying \[5{x^3} - 1\] by \[x\], the product of \[ - 1\] and \[x\] is \[ - x\]. Since the dividend has no term from which \[ - x\] can be subtracted, we have placed the term at the end of the dividend. Similarly, we have placed 3 at the end in the next step.
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
The shortest day of the year in India

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




