Question

Statement 1: The graph between velocity and displacement for a harmonic oscillator is an ellipse.
Statement 2: Velocity does not change uniformly with displacement in harmonic motion.
A) Statement 1 is false, statement 2 is true
B) Statement 1 is true, statement 2 is true, Statement 2 is the correct explanation for statement 1
C) Statement 1 is true, statement 2 is true, Statement 2 is not the correct explanation for statement 1
D) Statement 1 is false, statement 2 is false.

Answer 1

Hint: Velocity of a particle in a simple harmonic motion can be given in terms of amplitude, angular velocity and position of the particle. Squaring and dividing the equation accordingly, we can convert the equation into the equation for ellipse.
Formula used:
\[v=\omega \sqrt{{{a}^{2}}-{{x}^{2}}}\]

Complete step-by-step solution:
In a simple harmonic motion, velocity is given by,
\[v=\omega \sqrt{{{a}^{2}}-{{x}^{2}}}\]
Where,
\[\omega \]is the angular frequency
\[x\] is the position of the particle.
\[a\]is the amplitude of the particle
Then,
\[{{v}^{2}}={{\omega }^{2}}{{a}^{2}}-{{\omega }^{2}}{{x}^{2}}\] --------- 1
Dividing both sides of the equation 1 by \[{{\omega }^{2}}{{a}^{2}}\]
\[\dfrac{{{v}^{2}}}{{{\omega }^{2}}{{a}^{2}}}=1-\dfrac{{{\omega }^{2}}{{x}^{2}}}{{{\omega }^{2}}{{a}^{2}}}\]
\[\dfrac{{{v}^{2}}}{{{\omega }^{2}}{{a}^{2}}}+\dfrac{{{x}^{2}}}{{{a}^{2}}}=1\] ---------- 2

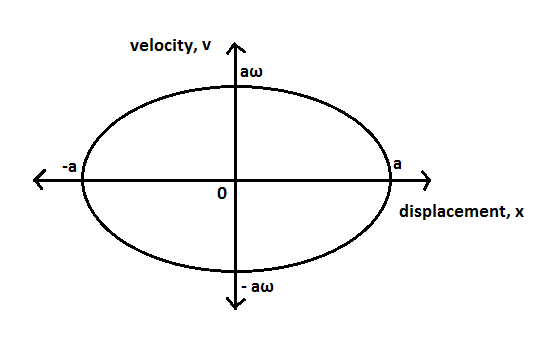
Velocity-displacement graph of a harmonic oscillator.
We have equation for ellipse as,
\[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\] ------------- 3
Comparing equations 2 and 3, we can say that the graph between velocity and displacement for a harmonic oscillator is an ellipse.
From the elliptical graph we can understand that the velocity is not changing uniformly with displacement in harmonic motion.
Hence, statement 1 is true, statement 2 is true, Statement 2 is not the correct explanation for statement 1.
Hence the answer is option C.

Note: The position of a particle in a simple harmonic motion is given by,
\[x=A\sin \omega t\]
Where,
\[A\] is the amplitude
\[\omega \] is the angular frequency
\[t\] is the time
Then,
\[\sin \omega t=\dfrac{x}{A}\]
Squaring the equation on both sides,
\[{{\sin }^{2}}\omega t=\dfrac{{{x}^{2}}}{{{A}^{2}}}\]
Velocity in a simple harmonic motion is given by,
\[v=A\omega \cos \omega t\]
Then,
\[\cos \omega t=\dfrac{v}{A\omega }\]
Squaring the equation on both sides,
\[{{\cos }^{2}}\omega t=\dfrac{{{v}^{2}}}{{{A}^{2}}{{\omega }^{2}}}\]
\[{{\sin }^{2}}\omega t+{{\cos }^{2}}\omega t=\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{v}^{2}}}{{{A}^{2}}{{\omega }^{2}}}\]
We have,
\[{{\sin }^{2}}x+{{\cos }^{2}}x=1\]
Then,
\[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{v}^{2}}}{{{A}^{2}}{{\omega }^{2}}}=1\] ---------- (1)
Equation for ellipse is given by, \[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\] ----------(2)
Comparing the equations 1 and 2 we can see that the graph between velocity and displacement for a harmonic oscillator is an ellipse.