Question

State whether the following statements are true or false. Give reasons for your answers.
 For any real number x, ${x^2} \geqslant 0$.
$
  (a){\text{ True}} \\
  {\text{(b) False}} \\
 $

Answer 1

Hint – If x is the domain of any function ${x^2}$ then try and substitute any negative value into ${x^2}$ to see whether it comes to be positive or not because eventually if we substitute any positive value in it its square will be positive only.

Complete step-by-step answer:

Given equation ${x^2} \geqslant 0$ for any real number x.

We have to show whether this statement is true or false.

Case (1) let us consider any positive real number say (x = 2).

So square the number we get,
$ \Rightarrow {x^2} = {2^2} = 4$……………….. (1)

And we all know 4 is greater than 0.
Case (2) let us consider x = 0
So 0 square is 0
$ \Rightarrow {x^2} = 0$……………………… (2)

Case (3) let us consider any negative real number say (x = -2)

So square the number we get,
$ \Rightarrow {x^2} = {\left( { - 2} \right)^2} = {\left( { - 1} \right)^2}{\left( 2 \right)^2} = \left( 1 \right)4 = 4$…………………………. (3)
And we all know 4 is greater than 0.

So in general from equation (1), (2) and (3) we can say that for any real number x, the square of x is always greater than or equal to zero.

$ \Rightarrow {x^2} \geqslant 0$ is true for any real number x.

Hence option (A) is correct.

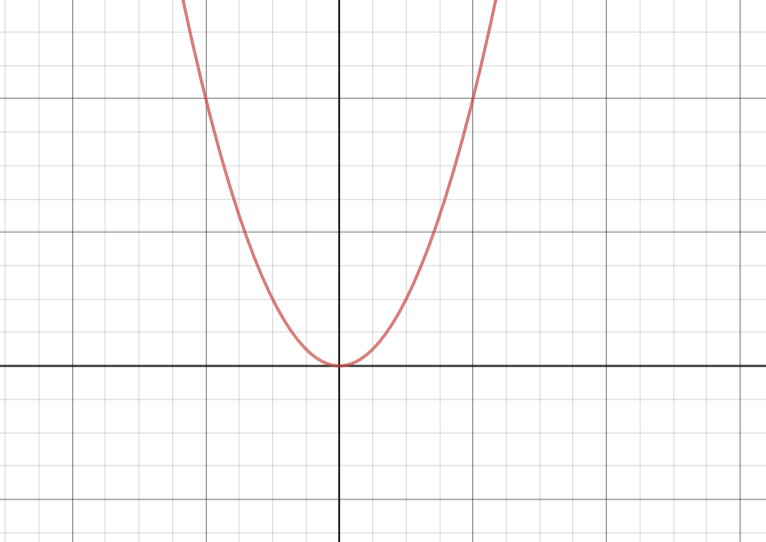
Note – There can be another method to prove this, graph of $y = {x^2}$ is a parabola opening upwards towards y axis, where y is the range and x is the domain of it, clearly from that graph no matter the value of x we substitute the y is always positive. This too proves the above mentioned. The graph is represented as