Question

State true or false: On a map drawn to a scale of \[1:25000\]; a triangular plot has the following measurements \[AB=3cm,BC=4cm\] and \[\angle ABC={{90}^{\circ }}\]. The area of the plot in sq.km is 37.5 sq.km.

Answer 1

Hint: We know that the scaling factor is equal to the ratio of length of model and length of building is equal to scale of the map. We know that the area of the triangle is equal to half of the product of base and height. By using these concepts, we can find the area of the plot.

Complete step by step answer:
We know that the scaling factor is equal to the ratio of length of model and length of building is equal to scale of the map. From the question, it is clear that the scale of the map is equal to \[1:25000\]. From the question, it is also clear that the following measurements \[AB=3cm,BC=4cm\].

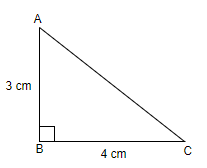
Let us consider
\[\begin{align}
  & AB=3cm...(1) \\
 & BC=4cm...(2) \\
\end{align}\]
\[x=\dfrac{1}{25000}....(3)\]
Let us assume the scale is equal to x. Let us assume the original length of AB is equal to ab. Let us assume the original length of BC is equal to bc.
\[\Rightarrow x=\dfrac{ab}{AB}....(4)\]
Let us substitute in equation (4) the value of AB from equation (1) and x from equation (3), then we get
\[\Rightarrow \dfrac{1}{25000}=\dfrac{3}{ab}\]
Now by using cross multiplication, we get
\[\begin{align}
  & \Rightarrow ab=\left( 25000 \right)\left( 3 \right)cm \\
 & \Rightarrow ab=75000cm....(5) \\
\end{align}\]
From equation (5), it is clear that the actual length of ab is equal to 75000 cm.
Let us substitute in equation (4) the value of BC from equation (2) and x from equation (3), then we get
\[\Rightarrow \dfrac{1}{25000}=\dfrac{4}{bc}\]
Now by using cross multiplication, we get
\[\begin{align}
  & \Rightarrow bc=\left( 25000 \right)\left( 4 \right) \\
 & \Rightarrow bc=100000cm....(6) \\
\end{align}\]
From equation (6), it is clear that the actual length of bc is equal to 100000 cm.
We know that 1 km is equal to 10000 cm.
Now from equation (5), we can get
\[\Rightarrow ab=0.75km....(7)\]
Now from equation (6), we can get
\[\Rightarrow bc=1km....(8)\]
We know that the area of the triangle is equal to half of the product of base and height. Let us assume the area of the triangle is equal to A, base of the triangle is equal to b and the height of the triangle is equal to h.
\[\Rightarrow A=\dfrac{1}{2}bh....(9)\]
From the diagram, it is clear that the area of triangle abc is equal to half of product of ab and bc.
\[\Rightarrow A=\dfrac{1}{2}(ab)(bc).....(10)\]
Now let us substitute equation (7) and equation (8) in equation (10), then we get
\[\begin{align}
  & \Rightarrow A=\dfrac{1}{2}\left( 0.75 \right)\left( 1 \right)k{{m}^{2}} \\
 & \Rightarrow A=0.375k{{m}^{2}}...(11) \\
\end{align}\]
So, from equation (7) it is clear that the area of the plot is equal to 0.375 sq.km.

Hence, the given statement is wrong.

Note: We know that the area of the triangle is equal to the product of base and height. Let us assume the area of the triangle is equal to A, base of the triangle is equal to b and the height of the triangle is equal to h \[A=bh\]. If this misconception is followed, then we cannot get correct answer. So, this misconception should be avoided.