Question

State the following statement is True or False
A parabolic arch has a height 18 meters and span 24 meters then the height of the arch at 8 meters from the center of the span is equal to 10.
A . True
B. False

Answer 1

Hint: We know that all the points on the parabola satisfy the equation of the parabola. Since one point of the parabola is given, substitute those values in the standard equation of parabola \[{x^2} = 4ay\] to find the value of 'a'. Later use the value of 'a' which was found to know the other coordinates.

Complete step-by-step answer:

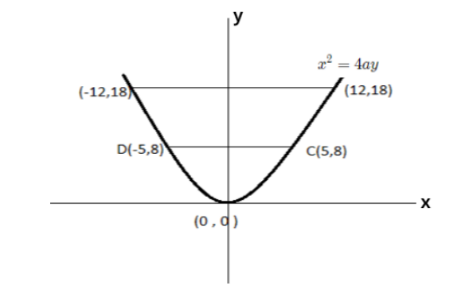
Satisfying all these points on the equation of parabola
\[{x^2} = 4ay\]
Given that the arch has a height of 18 meters and it spans 24 meters then according to the figure its end coordinates will be:
\[
  x = \pm 12 \\
  y = 18 \\
\]
Putting these values in the equation, as we know that the square of ( -12 ) & ( 12 ) is the same i.e 144.
\[
  {x^2} = 4ay \\
  144 = 4a \times 18 \\
  4a = 8 \\
  {x^2} = 8y \\
\]
Equation of the parabola is \[{x^2} = 8y\], height of arch for the span of 10.
Span of 10 means the coordinates of x-axis from the symmetrical axis are x = -5 & x = 5
\[x = \pm 5\] putting the value in equation \[{x^2} = 4ay\],
as we know that the square of ( -5 ) & ( 5 ) is same i.e 25
\[
  {x^2} = 8y \\
  25 = 4a \times y \\
  y = \dfrac{{25}}{8} \\
\]
Means for the span of 10, height of the arch is \[\dfrac{{25}}{8}\].

Hence the statement is False.

Note: A parabola is the locus of a point which moves in a plane, such that its distance from a fixed point (focus) is equal to its perpendicular distance from a fixed straight line , this straight line is called directrix of the parabola.