Question

State Newton’s Law of gravitation expresses it in vector form.

Answer 1

Hint: The Newton’s Law of gravitation is about the force of attraction that exists between all bodies in the universe. It tells us about how the force is dependent on certain parameters like mass, distance etc. The vector form is derived by expressing the vectors in a plane and then using their relations with each other.

Formula used:
 \[\text{F = }\dfrac{\text{G}{{\text{m}}_{\text{1}}}{{\text{m}}_{\text{2}}}}{{{\text{d}}^{\text{2}}}}\]
\[{{\vec{F}}_{12}}\text{ = -}\dfrac{\text{G}{{\text{m}}_{1}}{{\text{m}}_{2}}}{{{\text{r}}^{2}}}\text{ }{{\overset{\scriptscriptstyle\frown}{r}}_{21}}\]

Complete step-by-step answer:
Newton’s Law of Gravitation is a universal law which states that every particle in the universe attracts other particles with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between the centers of the two particles.
Let a particle of mass \[{{\text{m}}_{1}}\] attract another particle of mass \[{{\text{m}}_{2}}\]and the distance between the centers of both particles is\[\text{d}\]then force of gravitation,\[\text{F}\]between them is-
\[\text{F}\propto \dfrac{{{\text{m}}_{\text{1}}}{{\text{m}}_{\text{2}}}}{{{\text{d}}^{\text{2}}}}\]
On removing the proportionality sign, we get,

\[\text{F = }\dfrac{\text{G}{{\text{m}}_{\text{1}}}{{\text{m}}_{\text{2}}}}{{{\text{d}}^{\text{2}}}}\]
\[\text{G}\]is universal gravitational constant, it’s value is \[6.67\times {{10}^{-11}}\text{ }{{\text{m}}^{3}}\text{k}{{\text{g}}^{-1}}{{\text{s}}^{-2}}\] .
Let us consider two point masses A and B of mass \[{{\text{m}}_{1}}\] and \[{{\text{m}}_{2}}\] respectively. The distance between them is\[\text{r}\].

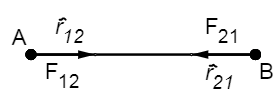
Here, \[{{\overset{\scriptscriptstyle\frown}{r}}_{12}}\] is the unit vector from A to B
\[{{\overset{\scriptscriptstyle\frown}{r}}_{21}}\] is the unit vector from B to A
\[{{\vec{F}}_{12}}\] is the force of gravitation exerted by A on B
\[{{\vec{F}}_{21}}\] is the force of gravitation exerted by B on A
By Newton’s Law of Gravitation, we know that,
\[{{\vec{F}}_{12}}\text{ }=\text{ }\dfrac{G{{m}_{1}}{{m}_{2}}}{{{r}^{2}}}\text{ }{{\overset{\scriptscriptstyle\frown}{r}}_{12}}\]
\[{{\vec{F}}_{21}}\text{ }=\text{ }\dfrac{G{{m}_{1}}{{m}_{2}}}{{{r}^{2}}}\text{ }{{\overset{\scriptscriptstyle\frown}{r}}_{21}}\]
As \[{{\vec{F}}_{12}}\]and \[{{\vec{F}}_{21}}\]are attractive forces, so their directions are opposite to each other. Therefore,
\[{{\vec{F}}_{12}}\text{ }=\text{ }-\text{ }{{\vec{F}}_{21}}\]
 \[{{\vec{F}}_{12}}\text{ }=\text{ }-\dfrac{G{{m}_{1}}{{m}_{2}}}{{{r}^{2}}}\text{ }{{\overset{\scriptscriptstyle\frown}{r}}_{21}}\]
As we know,
\[r\text{ }=\text{ }\left| {{{\overset{\scriptscriptstyle\frown}{r}}}_{12}} \right|\text{ }=\text{ }\left| {{{\overset{\scriptscriptstyle\frown}{r}}}_{21}} \right|\]
\[{{\vec{F}}_{12}}\text{ }=\text{ }-\dfrac{G{{m}_{1}}{{m}_{2}}}{{{\left| {{{\vec{r}}}_{21}} \right|}^{2}}}\text{ }{{\overset{\scriptscriptstyle\frown}{r}}_{21}}\] - (1)
\[{{\vec{F}}_{12}}\text{ }=\text{ }-\dfrac{G{{m}_{1}}{{m}_{2}}}{{{\left| {{{\vec{r}}}_{12}} \right|}^{2}}}\text{ }{{\overset{\scriptscriptstyle\frown}{r}}_{12}}\text{ }=\text{ }{{\vec{F}}_{12}}\text{ }=\text{ }\dfrac{G{{m}_{1}}{{m}_{2}}}{{{\left| {{{\vec{r}}}_{21}} \right|}^{2}}}\text{ }{{\overset{\scriptscriptstyle\frown}{r}}_{21}}\text{ }[\because \text{ }{{\overset{\scriptscriptstyle\frown}{r}}_{12}}\text{ }=\text{ }-\text{ }{{\overset{\scriptscriptstyle\frown}{r}}_{21}}]\] - (2)
From eq (1) and eq (2), we have,
\[{{\vec{F}}_{12}}\text{ }=\text{ }-\text{ }{{\vec{F}}_{21}}\]

 From the above figure,
\[{{\vec{r}}_{12}}\text{ }=\text{ }{{\vec{r}}_{2}}\text{ }-\text{ }{{\vec{r}}_{1}}\]

\[{{\overset{\scriptscriptstyle\frown}{r}}_{12}}\text{ }=\text{ }\dfrac{{{{\vec{r}}}_{2}}\text{ }-\text{ }{{{\vec{r}}}_{1}}}{\left| {{{\vec{r}}}_{2}}\text{ }-\text{ }{{{\vec{r}}}_{1}} \right|}\] - (3)
Substituting eq (3) in eq (1)

 \[{{\vec{F}}_{12}}\text{ }=\text{ }-\dfrac{G{{m}_{1}}{{m}_{2}}}{{{\left| {{{\vec{r}}}_{2}}-{{{\vec{r}}}_{1}} \right|}^{3}}}\text{ }({{\vec{r}}_{2}}\text{ }-\text{ }{{\vec{r}}_{1}})\]

To summarize, Newton’s Law of gravitation states that every particle in the universe attracts every other particle with the force such that, \[\text{F}\propto \dfrac{{{\text{m}}_{\text{1}}}{{\text{m}}_{\text{2}}}}{{{\text{d}}^{\text{2}}}}\] and it’s vector form is \[{{\vec{F}}_{12}}\text{ }=\text{ }-\dfrac{G{{m}_{1}}{{m}_{2}}}{{{\left| {{{\vec{r}}}_{2}}-{{{\vec{r}}}_{1}} \right|}^{3}}}\text{ }({{\vec{r}}_{2}}\text{ }-\text{ }{{\vec{r}}_{1}})\]

Note: Gravitational forces on two given bodies are opposite in direction but equal in magnitude. Vectors are quantities which have magnitude as well as direction. The unit vector is given by \[\overset{\scriptscriptstyle\frown}{r}\text{ }=\text{ }\dfrac{{\vec{r}}}{\left| {\vec{r}} \right|}\] .Gravitational forces are always attractive in nature and are one of the weakest forces.