Question

State and prove the parallelogram law of vector addition.

Answer 1

Hint: First write the parallelogram law for normal parallelogram then write the same for vectors. Find the equation for the addition of vectors when they are acting from a point in the shape of a parallelogram. Then try to derive that equation from the parallelogram vector diagram.

Complete answer:
The parallelogram law states that the sum of the squares of the length of the two diagonals is equal to the sum of the squares of the length of the four sides of the parallelogram.

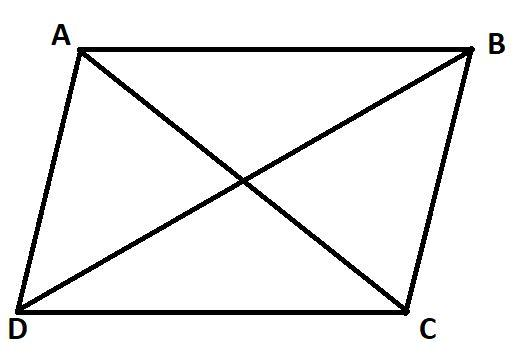
In the above diagram, ABCD is a parallelogram, wherein sides AB and DC are equal, and AD and BC are also equal. So if we apply the parallelogram law then,
$2{(AB)^2} + 2{(BC)^2} = {(AC)^2} + {(BD)^2}$,
If the parallelogram is a rectangle then the law will be,
$2{(AB)^2} + 2{(BC)^2} = 2{(AC)^2}$,
Because in the case of rectangle diagonals are of equal length(AC=BD).
Now coming to the part of the parallelogram law of vector addition.
The parallelogram law of vector addition states that if two vectors act simultaneously at the same point, then that vector can be represented both in magnitude by the diagonal or by the direction of the parallelogram passing through the point.

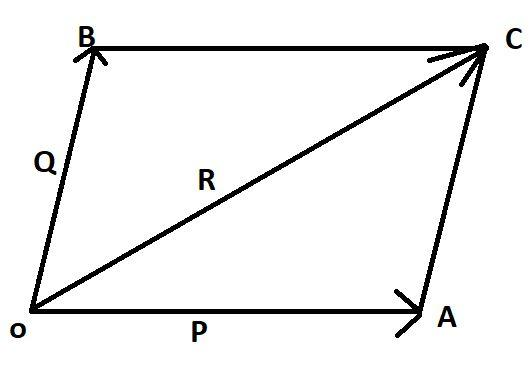
Here AOBC is a parallelogram, Q (BO) and P(OA) are two vectors acting from a point and R(OC) is the resultant vector.
 So according to the parallelogram law,
$\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} $, or we can say
$\vec P + \vec Q = \vec R$.
Prove For parallelogram law.
The Law of cosine also known as the cosine rule actually related all three sides of a triangle with an angle of it. If two sides and an angle are given for a triangle then we can find the other side using the cosine rule.
In a parallelogram, if we see carefully we can see that there are triangles in a parallelogram.

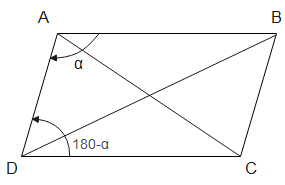
Let, x=AD=BC, y=AB=DC and $\angle BAD = \alpha $
Now using the law of cosines in the triangle BAD, we get
$B{D^2} = A{D^2} + A{B^2} - 2\left( {AD} \right)\left( {AB} \right)\cos \left( \alpha \right)$
But we have AB=y and AD=x. Substituting these values in the above equation and rearranging the terms will give us the below equation
${x^2} + {y^2} - 2xy\cos \alpha = B{D^2}$ ….. eq.1
 We know that in a parallelogram, the adjacent angles are supplementary, so we can say $\angle ADC = 180 - \alpha $,
Applying the law of cosines in triangle ADC,
$A{C^2} = A{D^2} + C{D^2} - 2\left( {AD} \right)\left( {CD} \right)\cos \left( {180 - \alpha } \right)$
But we have CD=y and AD=x. Substituting these values in the above equation and rearranging the terms will give us the below equation
${x^2} + {y^2} - 2xy\cos (180 - \alpha ) = A{C^2}$ ……eq.2
${x^2} + {y^2} + 2xy\cos (\alpha ) = A{C^2}$(as cos (180-x)=-cos x)
Now, if we represent the sum of the squares of the diagonal,
$\left( {B{D^2} + A{C^2}} \right) = {x^2} + {y^2} - 2xy\cos \alpha + {x^2} + {y^2} + 2xy\cos \alpha $
Now on simplifying the above equation we get,
$\left( {B{D^2} + A{C^2}} \right) = 2{x^2} + 2{y^2}$…. Eq.3
This equation number 3 can be represented as,
$\left( {B{D^2} + A{C^2}} \right) = 2{(AB)^2} + 2{(BC)^2}$,
Hence parallelogram law is proved.

Note:
It is necessary that all the sides of the parallelogram should have equal and opposite sides. The terms that had to be changed must be known as it is not possible in the examination hall to try and test each and every method. Students must remember the law of cosine. They must know how the parallelogram is to be calculated to get the required result.