Question

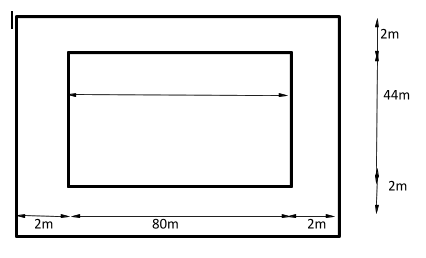
How many square tiles of side 40cm will be required to pave a footpath which is 2m wide and surrounds a rectangular plot 80m by 44m?

Answer 1

Hint: We will find the area of the footpath by subtracting the area of the outer fence to the area of the rectangular plot.
Then we will find the number of tiles required by dividing the area of the footpath to the area of a single tile.

Complete step by step solution: Given:
\[
  {\text{Dimensions of rectangular plot = 80m} \times \text{40m}} \\
  {\text{Width of foot path = 2m}} \\
  {\text{Side of square tile = 40cm}} \\
 \]

\[{\text{Area of rectangle = (length)(breadth)}}\]
\[
  {\text{Area of outer rectangular plot = (80 + 2 + 2)(44 + 2 + 2)}} \\
  {\text{ = (84)(48)}} \\
  {\text{ = 4032}}{{\text{m}}^{\text{2}}} \\
 \]
\[
  {\text{Area of rectangular plot (inner rectangle) = (80)(44)}} \\
  {\text{ = 3520}}{{\text{m}}^{\text{2}}} \\
 \]
\[
  {\text{Area of footpath = Area of outer rectangular plot - Area of rectangular plot (inner rectangle)}} \\
  {\text{ = 4032 - 3520}} \\
  {\text{ = 512}}{{\text{m}}^{\text{2}}} \\
 \]
\[
  {\text{Area of square = (side}}{{\text{)}}^{\text{2}}} \\
  {\text{1cm = 1}}{{\text{0}}^{{\text{ - 2}}}}{\text{m}} \\
  {\text{Area of a single square tile = 4}}{{\text{0}}^{\text{2}}} \\
  {\text{ = 1600c}}{{\text{m}}^{\text{2}}} \\
  {\text{ = 1600(1}}{{\text{0}}^{{\text{ - 4}}}}{\text{)}}{{\text{m}}^{\text{2}}} \\
  {\text{ = }}\dfrac{{{\text{16}}}}{{{\text{100}}}}{{\text{m}}^{\text{2}}} \\
  {\text{ = }}\dfrac{{\text{4}}}{{{\text{25}}}}{{\text{m}}^{\text{2}}} \\
 \]
\[{\text{Number of tiles = }}\dfrac{{{\text{Area of footpath}}}}{{{\text{Area of a single square tile}}}}\]
\[
  {\text{Number of tiles = }}\dfrac{{{\text{512}}}}{{\dfrac{{\text{4}}}{{{\text{25}}}}}} \\
  {\text{ = }}\dfrac{{{\text{512}}}}{{\text{4}}}{\text{(25)}} \\
  {\text{ = 3200}} \\
 \]

Therefore, 3200 square tiles are required to pave the footpath.

Note: We can also find this answer by finding the number of tiles of distinction that can be paved in total and the number of tiles that can be paved in the rectangular plot.
 \[
  {\text{total number of tiles = }}\dfrac{{{\text{total area}}}}{{{\text{Area of a single square tile}}}} \\
  {\text{ = }}\dfrac{{{\text{4032}}}}{{\dfrac{{\text{4}}}{{{\text{25}}}}}} \\
  {\text{ = 25200}} \\
 \]
\[
  {\text{number of tiles can be paved in plot = }}\dfrac{{{\text{plot area}}}}{{{\text{Area of a single square tile}}}} \\
  {\text{ = }}\dfrac{{{\text{3520}}}}{{\dfrac{{\text{4}}}{{{\text{25}}}}}} \\
  {\text{ = 22000}} \\
 \]
Therefore, by subtracting the number of tiles that can be paved in the plot to the number of tiles that can be paved in the total area we will get the number of tiles that can be paved in the footpath.
\[
  {\text{numbers of tiles required = 25200 - 22000}} \\
  {\text{ = 3200}} \\
 \]