Question

$\sqrt {\dfrac{{1 + \sin A}}{{1 - \sin A}}} = \sec A + \tan A$, then, A lies in the quadrants
A) I, II
B) II, III
C) I, IV
D) III, V

Answer 1

Hint:
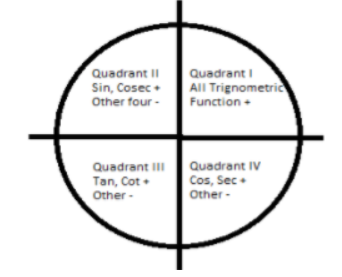
When two lines with a real axis and imaginary axis pass perpendicular through a circle, the circle divides itself into four quadrants. By analysing the quadrants, we get quadrant I with both x and y-axis are positive, Quadrant II with x-axis is negative, and the y-axis is positive, Quadrant III with both the x-axis and y-axis are negative, and in Quadrant IV with x-axis is positive, and the y-axis is negative.
Now when we talk about trigonometric functions then in quadrant I, all the functions remains positive, in Quadrant II, only sin and cosec functions are positive, while other functions are negative, in Quadrant III, only tan and cot functions are positive while others are negative, and in the case of Quadrant IV, only cos and sec functions are positive while others being negative.

Complete step by step solution:
 $\sqrt {\dfrac{{1 + \sin A}}{{1 - \sin A}}} = \sec A + \tan A$
To remove the square root, we are going to rationalize numerator and denominator by multiplying then with the same rational number. hence by rationalizing the L.H.S. of the given function, we get:
 $ \Rightarrow \sqrt {\dfrac{{1 + \sin A}}{{1 - \sin A}}} = \sqrt {\dfrac{{\left( {1 + \sin A} \right)\left( {1 + \sin A} \right)}}{{\left( {1 - \sin A} \right)\left( {1 + \sin A} \right)}}} $
$ \Rightarrow \sqrt {\dfrac{{1 + \sin A}}{{1 - \sin A}}} = \sqrt {\dfrac{{{{\left( {1 + \sin A} \right)}^2}}}{{\left( {1 - {{\sin }^2}A} \right)}}} $
$ \Rightarrow \sqrt {\dfrac{{1 + \sin A}}{{1 - \sin A}}} = \dfrac{{\left( {1 + \sin A} \right)}}{{\sqrt {\left( {{{\cos }^2}A} \right)} }}{\text{ }}\left[ {\because {{\sin }^2}A + {{\cos }^2}A = 1} \right]$
 $ \Rightarrow \sqrt {\dfrac{{1 + \sin A}}{{1 - \sin A}}} = \dfrac{{\left( {1 + \sin A} \right)}}{{\left| {\cos A} \right|}}$
Hence, we have got the LHS as: $\dfrac{{\left( {1 + \sin A} \right)}}{{\left| {\cos A} \right|}}$
We know$\sqrt {\left( {{{\cos }^2}A} \right)} = \left| {\cos A} \right| = \pm \cos A$, hence we put the value $ + \cos A$and $ - \cos A$to check the function:
$\dfrac{{\left( {1 + \sin A} \right)}}{{\left| {\cos A} \right|}} = \dfrac{1}{{ + \cos A}} + \dfrac{{\sin A}}{{ + \cos A}} = \sec A + \tan A - - - - (i)$
$\dfrac{{\left( {1 + \sin A} \right)}}{{\left| {\cos A} \right|}} = \dfrac{1}{{ - \cos A}} + \dfrac{{\sin A}}{{ - \cos A}} = - \sec A - \tan A - - - - (ii)$
Hence, we can see in equation (i) $ + \cos A$ satisfies the given equation, $\cos A$is positive only in quadrant I and quadrant IV.

Therefore, option (C) is the correct answer.

Note:
The trigonometric cofunction identities provide the relationship between the sin, cos, tan, cosine, sec, and cot function. The value of the trigonometric function for an angle is equal to the value of the cofunction of the complement.