Question

How do you solve ${x^2} + 4x + 4 \geqslant 9$ using a sign chart?

Answer 1

Hint: We will first bring all the terms to the left hand side and then factorize the quadratic equation thus obtained. After that, we will just find the values where it takes positive values.

Complete step-by-step solution:
We are given that we are required to solve ${x^2} + 4x + 4 \geqslant 9$ using a sign chart.
We have the expression given by the equation: ${x^2} + 4x + 4 \geqslant 9$
Taking 9 from addition in the right hand side to subtraction in the left hand side, we will then obtain the following equation with us:-
$ \Rightarrow {x^2} + 4x + 4 - 9 \geqslant 0$
Simplifying the terms on the left hand side of the above expression, we will then obtain the following equation with us:-
$ \Rightarrow {x^2} + 4x - 5 \geqslant 0$
Now, we can also write this as:-
$ \Rightarrow {x^2} - x + 5x - 5 \geqslant 0$
Taking x common from the first two terms in the left hand side of the above expression, we will then obtain the following equation with us:-
$ \Rightarrow x(x - 1) + 5x - 5 \geqslant 0$
Taking 5 common from the last two terms in the left hand side of the above expression, we will then obtain the following equation with us:-
$ \Rightarrow x(x - 1) + 5(x - 1) \geqslant 0$
Now, since (x – 1) is common in both of the terms, we can take it common and will obtain the following expression with us:-
$ \Rightarrow (x - 1)(x + 5) \geqslant 0$
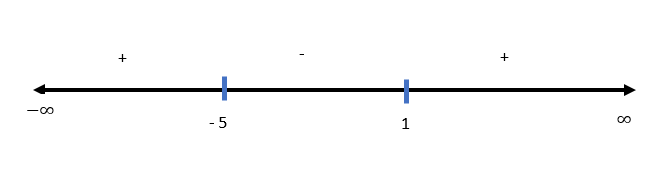
Now, we see that the points where the expression takes the value 0 will be 1 and – 5.
Now, we see that sign chart as follows:-
Now, we need to see what value the function takes.
Case 1: We have the first interval as $\left( { - \infty , - 5} \right)$.
Let us for instance put x = - 6 and see that the function turns out to be:-
$ \Rightarrow (x - 1)(x + 5) = ( - 6 - 1)( - 6 + 5)$
$ \Rightarrow (x - 1)(x + 5) = 7$ which is greater than zero.
Therefore, this interval is in the answer.
Case 2: We have the first interval as $\left( { - 5,1} \right)$.
Let us for instance put x = 0 and see that the function turns out to be:-
$ \Rightarrow (x - 1)(x + 5) = (0 - 1)(0 + 5)$
$ \Rightarrow (x - 1)(x + 5) = - 5$ which is less than zero.
Therefore, this interval cannot be in the answer.
Case 3: We have the first interval as $\left( {1,\infty } \right)$.
Let us for instance put x = 2 and see that the function turns out to be:-
$ \Rightarrow (x - 1)(x + 5) = (2 - 1)(2 + 5)$
$ \Rightarrow (x - 1)(x + 5) = 7$ which is greater than zero.
Therefore, this interval is in the answer.

Hence, the required answer is $x \in \left( { - \infty , - 5} \right) \cup \left( {1,\infty } \right)$.

Note: The students must note that while pursuing the sign chart, we have used a hidden theorem which states that: If $a.b \geqslant 0$, then there are two possible cases given as follows:-
$a \geqslant 0$ and $b \geqslant 0$
$a \leqslant 0$ and $b \leqslant 0$
We eventually got the following sign chart as the answer:-