Question

How do you solve the triangles when it has a hypotenuse of 18, the opposite angle is the height and the adjacent meets the hypotenuse at ${{35}^{\circ }}$. Find the other sides and measurement of angles.

Answer 1

Hint: We first find the hypotenuse and its opposite angles. We have been given one side’s length and two angle values. We use those in the equation \[\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}\] to find other measurements.

Complete step by step solution:
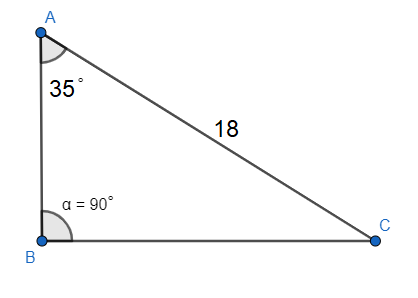
We have been given the values of one side’s length and measurement of two angles.
We are going to use the relation for properties of triangles between angles and sides of a general triangle.
The relation gives that for $\Delta ABC$, we have \[\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}\] where $a,b,c$ are the lengths of the sides and $A,B,C$ are corresponding opposite angles of the sides $a,b,c$ respectively.
The hypotenuse be b where $b=18$ and $\angle A={{35}^{\circ }},\angle B={{90}^{\circ }}$.

We now find the third angle using the relation of the angles of a triangle where we get the sum of all the angles as ${{180}^{\circ }}$.
So, $\angle A+\angle B+\angle C={{180}^{\circ }}$ which gives $\angle C={{180}^{\circ }}-\angle A-\angle B$.
We put the values to get \[\angle C={{180}^{\circ }}-{{35}^{\circ }}-{{90}^{\circ }}={{55}^{\circ }}\].
We put these values in the equation \[\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}\] to get \[\dfrac{a}{\sin {{35}^{\circ }}}=\dfrac{18}{\sin {{90}^{\circ }}}=\dfrac{c}{\sin {{55}^{\circ }}}\]
Simplifying we get \[\sin {{90}^{\circ }}=1,\sin {{35}^{\circ }}=0.5735,\sin {{55}^{\circ }}=0.8191\].
So, \[\dfrac{a}{0.5735}=\dfrac{18}{1}=\dfrac{c}{0.8191}\]
Solving the equation, we get \[c=18\times 0.8191=14.744\] and \[a=18\times 0.5735=10.324\].
Therefore, the other angle is \[\angle C={{55}^{\circ }}\] and the other sides are \[c=14.744,a=10.324\].

Note: We need to remember that the main relation of the ratios is with $2R$ where $R$ is the circum-radius of the triangle. So, the relation is \[\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R\]. We can also express the $R$ as $2R=\dfrac{abc}{2\Delta }$ where $\Delta =\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$, the area of the triangle.