
How do you solve the triangle given $B={{2}^{\circ }}45',b=6.2,c=5.8$ ?
Answer
537k+ views
Hint: At first we convert the minutes to degrees for easier calculations. Then, we apply the Lami’s theorem which is $\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}$ . After putting the known values in the Lami’s theorem formula, we get the required values.
Complete step by step solution:
The details that we have been provided about the triangle $\Delta ABC$ are that
$B={{2}^{\circ }}45',b=6.2,c=5.8$
At first we convert the angle into degrees completely by dividing by $60$ . We get,
${{2}^{\circ }}45'={{\left( 2+\dfrac{45}{60} \right)}^{\circ }}={{2.75}^{\circ }}$
We can see that as we are given the length of a side and its opposite angle, we can easily apply the Lami’s theorem. Lami's theorem states that for any triangle $\Delta ABC$ , if $a,b,c$ are the three sides of the triangle and $A,B,C$ are the three angles, then there is a formula which relates all of them. This formula is,
$\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}$
This huge equation can be broken down into two equations, which are
$\dfrac{c}{\sin \angle C}=\dfrac{b}{\sin \angle B}....\left( 1 \right)$
$\dfrac{a}{\sin \angle A}=\dfrac{b}{\sin \angle B}....\left( 2 \right)$
Let us first solve the equation $\left( 1 \right)$ . We put the values of $c,b,B$ in the equation to get,
$\Rightarrow \dfrac{5.8}{\sin C}=\dfrac{6.2}{\sin {{2.75}^{\circ }}}$
Taking reciprocals on both sides of the above equation, we get,
$\Rightarrow \dfrac{\sin C}{5.8}=\dfrac{\sin {{2.75}^{\circ }}}{6.2}$
Multiplying both sides of the above equation by $5.8$ , we get,
$\Rightarrow \sin C=\dfrac{\sin {{2.75}^{\circ }}}{6.2}\times 5.8$
Upon simplification, we get,
$\Rightarrow \sin C=\dfrac{0.0479}{1.0689}$
This gives,
$\Rightarrow \sin C=0.0448$
Taking ${{\sin }^{-1}}$ on both sides, we get,
$\begin{align}
& \Rightarrow C={{\sin }^{-1}}\left( 0.0448 \right) \\
& \Rightarrow C={{2.5684}^{\circ }}={{2}^{\circ }}+\left( 60\times 0.5684 \right)'={{2}^{\circ }}34.106' \\
\end{align}$
Let us now solve the equation $\left( 2 \right)$ . But, there are two unknowns and only one equation available. Thus, we have to incorporate a second equation, which is the sum of internal angles of a triangle,
$A+B+C={{180}^{\circ }}$
Putting the values of $B,C$ in the above equation, we get,
$\begin{align}
& \Rightarrow A+{{2.75}^{\circ }}+{{2.5684}^{\circ }}={{180}^{\circ }} \\
& \Rightarrow A={{174.6816}^{\circ }}={{174}^{\circ }}+\left( 0.6816\times 60 \right)'={{174}^{\circ }}40.896' \\
\end{align}$
We can now solve the equation $\left( 2 \right)$ easily. Putting the values of $\angle C,\angle B,b$ ,we get,
$\begin{align}
& \Rightarrow \dfrac{a}{\sin {{174.6816}^{\circ }}}=\dfrac{6.2}{\sin {{2.75}^{\circ }}} \\
& \Rightarrow a=\dfrac{6.2}{\sin {{2.75}^{\circ }}}\times \sin {{174.6816}^{\circ }} \\
& \Rightarrow a=11.9779 \\
\end{align}$
Therefore, we can conclude that the triangle $\Delta ABC$ has the angles $A={{174}^{\circ }}40.896',B={{2}^{\circ }}45',C={{2}^{\circ }}34.106'$ and the sides $a=11.9779,b=6.2,c=5.8$.
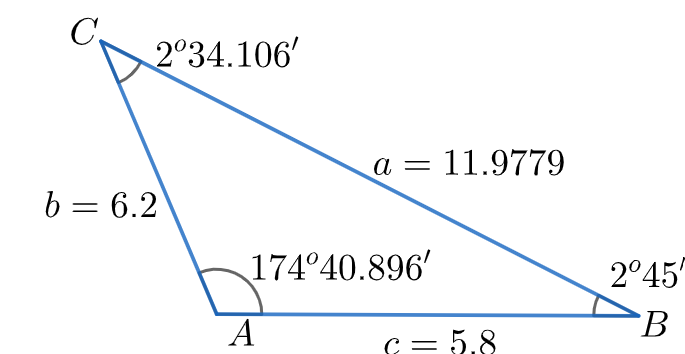
Note: While converting the minutes into degrees, we must be careful and should not instead multiply it with $60$ . Also, we can convert the degrees into minutes, according to our ease. While applying the Lamis’ theorem, we should only use $\text{sine}$ and no other trigonometric ratio.
Complete step by step solution:
The details that we have been provided about the triangle $\Delta ABC$ are that
$B={{2}^{\circ }}45',b=6.2,c=5.8$
At first we convert the angle into degrees completely by dividing by $60$ . We get,
${{2}^{\circ }}45'={{\left( 2+\dfrac{45}{60} \right)}^{\circ }}={{2.75}^{\circ }}$
We can see that as we are given the length of a side and its opposite angle, we can easily apply the Lami’s theorem. Lami's theorem states that for any triangle $\Delta ABC$ , if $a,b,c$ are the three sides of the triangle and $A,B,C$ are the three angles, then there is a formula which relates all of them. This formula is,
$\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}$
This huge equation can be broken down into two equations, which are
$\dfrac{c}{\sin \angle C}=\dfrac{b}{\sin \angle B}....\left( 1 \right)$
$\dfrac{a}{\sin \angle A}=\dfrac{b}{\sin \angle B}....\left( 2 \right)$
Let us first solve the equation $\left( 1 \right)$ . We put the values of $c,b,B$ in the equation to get,
$\Rightarrow \dfrac{5.8}{\sin C}=\dfrac{6.2}{\sin {{2.75}^{\circ }}}$
Taking reciprocals on both sides of the above equation, we get,
$\Rightarrow \dfrac{\sin C}{5.8}=\dfrac{\sin {{2.75}^{\circ }}}{6.2}$
Multiplying both sides of the above equation by $5.8$ , we get,
$\Rightarrow \sin C=\dfrac{\sin {{2.75}^{\circ }}}{6.2}\times 5.8$
Upon simplification, we get,
$\Rightarrow \sin C=\dfrac{0.0479}{1.0689}$
This gives,
$\Rightarrow \sin C=0.0448$
Taking ${{\sin }^{-1}}$ on both sides, we get,
$\begin{align}
& \Rightarrow C={{\sin }^{-1}}\left( 0.0448 \right) \\
& \Rightarrow C={{2.5684}^{\circ }}={{2}^{\circ }}+\left( 60\times 0.5684 \right)'={{2}^{\circ }}34.106' \\
\end{align}$
Let us now solve the equation $\left( 2 \right)$ . But, there are two unknowns and only one equation available. Thus, we have to incorporate a second equation, which is the sum of internal angles of a triangle,
$A+B+C={{180}^{\circ }}$
Putting the values of $B,C$ in the above equation, we get,
$\begin{align}
& \Rightarrow A+{{2.75}^{\circ }}+{{2.5684}^{\circ }}={{180}^{\circ }} \\
& \Rightarrow A={{174.6816}^{\circ }}={{174}^{\circ }}+\left( 0.6816\times 60 \right)'={{174}^{\circ }}40.896' \\
\end{align}$
We can now solve the equation $\left( 2 \right)$ easily. Putting the values of $\angle C,\angle B,b$ ,we get,
$\begin{align}
& \Rightarrow \dfrac{a}{\sin {{174.6816}^{\circ }}}=\dfrac{6.2}{\sin {{2.75}^{\circ }}} \\
& \Rightarrow a=\dfrac{6.2}{\sin {{2.75}^{\circ }}}\times \sin {{174.6816}^{\circ }} \\
& \Rightarrow a=11.9779 \\
\end{align}$
Therefore, we can conclude that the triangle $\Delta ABC$ has the angles $A={{174}^{\circ }}40.896',B={{2}^{\circ }}45',C={{2}^{\circ }}34.106'$ and the sides $a=11.9779,b=6.2,c=5.8$.
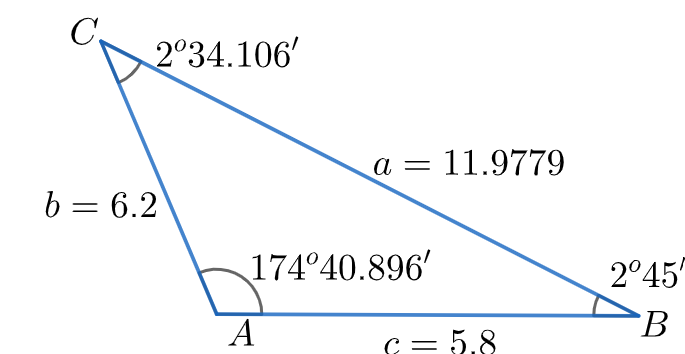
Note: While converting the minutes into degrees, we must be careful and should not instead multiply it with $60$ . Also, we can convert the degrees into minutes, according to our ease. While applying the Lamis’ theorem, we should only use $\text{sine}$ and no other trigonometric ratio.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Who was the first woman to receive Bharat Ratna?

Write a letter to the principal requesting him to grant class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Discuss the main reasons for poverty in India




