Question

How do you solve the triangle given \[A={{36}^{\circ }},a=8,b=5\]?

Answer 1

Hint: From the question we are given one angle and two sides of a triangle and we are asked to find the remaining angles and sides of the respected triangle. To solve the question we will use the sine rule and find the angle B and after we will find the other angle by subtracting the \[A+B\] angle from the total angle of a triangle which is \[180\] degree and again we use the sine rule and find all the sides and angles.

Complete step by step solution:
The reference says that \[a>b\] then one possible triangle exists.
We are given the question that \[A={{36}^{\circ }},a=8,b=5\].

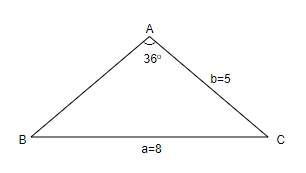
We will find the angle B by using the sine rule which is as follows.
\[\Rightarrow \dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c}\]
We use the formula and find angle B as follows.
\[\Rightarrow \dfrac{\sin A}{a}=\dfrac{\sin B}{b}\]
\[\Rightarrow \sin B=\dfrac{\sin A}{a}\times (b)\]
\[\Rightarrow B={{\sin }^{-1}}\left( \dfrac{\sin A}{a}\times (b) \right)\]
\[\Rightarrow B={{\sin }^{-1}}\left( \dfrac{\sin 36}{8}\times (5) \right)\]
\[\Rightarrow B\simeq {{21.55}^{\circ }}\]
Here we found out the angle B.
Now we know that the total angle in a triangle is \[180\].
So, we will find the remaining angle which is C by subtracting the total A and B angle from the total angle of a triangle which is \[180\].
So, we get the following.
 \[\Rightarrow C\simeq {{180}^{\circ }}-{{21.55}^{\circ }}-{{36}^{\circ }}\]
\[\Rightarrow C\simeq {{122.45}^{\circ }}\]
We will use the sine law and find the remaining side c as follows.
\[\Rightarrow \dfrac{\sin A}{a}=\dfrac{\sin C}{c}\]
\[\Rightarrow c=\dfrac{\sin {{122.45}^{\circ }}}{\sin {{36}^{\circ }}}\times 8\]
\[\Rightarrow c\simeq 11.49\]

Note: Students should be very careful in doing the calculations. Students should be able to co relate the triangles concept with the trigonometric concept. Students should know the sine rule for solving the question which is as follows.
 \[\Rightarrow \dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c}\]