Question

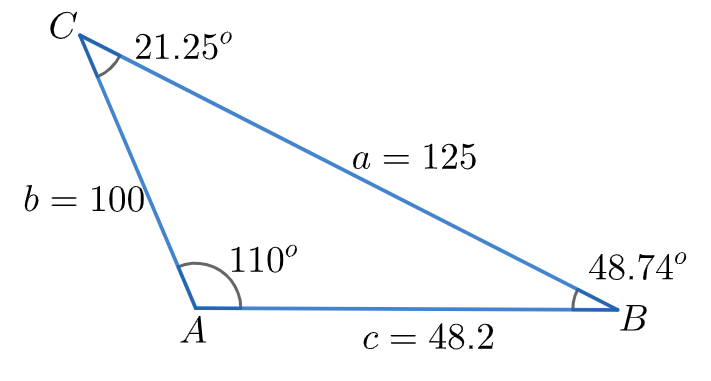
How do you solve the triangle given $A={{110}^{\circ }}$ , $a=125$ , $b=100$ ?

Answer 1

Hint: Problems on determining the triangle can be solved either by using the Law of cosines or by using the Law of Sines. As, we are given two sides of the triangle along with the angle opposite of the side $a$ we use the Law of Sines. Using the Law of Sines, we first consider the two terms only related to $a\text{ and }b$ . From there we get the value of the angle $B$which in turn gives the value of angle $C$ . Further, using the sine law we obtain the side $c$ .

Complete step by step solution:
We are given that $A={{110}^{\circ }}$ , $a=125$ , $b=100$
For this case we must use the Law of sines as we are given two sides of the triangle along with the angle opposite of the side $a$ .
According to the Law of sines
$\dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c}$
Foe now we only consider the part $\dfrac{\sin A}{a}=\dfrac{\sin B}{b}$
Substituting the values in the above equation we get
$\Rightarrow \dfrac{\sin {{110}^{\circ }}}{125}=\dfrac{\sin B}{100}$
Further simplifying we get
$\Rightarrow \sin B=\dfrac{\sin {{110}^{\circ }}}{125}\times 100$
$\Rightarrow \sin B=0.7518$
Taking sin inverse on both the sides of the above equation we get
$\Rightarrow B={{\sin }^{-1}}\left( 0.7518 \right)$
$\Rightarrow B={{48.74}^{\circ }}$
Now, we have values of two angles and we know that the summation of all the internal angle of a triangle is ${{180}^{\circ }}$
Hence, we subtract the summation of the two angles from $180$ which gives us the value of the other angle $C$ as
$\Rightarrow C=180-\left( B+A \right)$
Substituting the values in the above formula, we get
$\Rightarrow C=180-\left( 48.74+110 \right)$
$\Rightarrow C={{21.26}^{\circ }}$
Now, we again consider the law of sines as
$\Rightarrow \dfrac{\sin A}{a}=\dfrac{\sin C}{c}$
Substituting the values in the above equation, we get
$\Rightarrow \dfrac{\sin {{110}^{\circ }}}{125}=\dfrac{\sin {{21.26}^{\circ }}}{c}$
Simplifying the above equation, we get
\[\Rightarrow c=\sin {{21.26}^{\circ }}\times \dfrac{125}{sin{{110}^{\circ }}}\]
\[\Rightarrow c=0.362\times \dfrac{125}{0.939}\]
\[\Rightarrow c=48.189\]
Therefore, in the triangle \[A={{110}^{\circ }},B={{48.74}^{\circ }},C={{21.25}^{\circ }}\] , and \[a=125,b=100,c=48.2\].

Note: While doing a problem we must decide properly where to use the Laws of cosines and where to use the Laws of sines so that no mistakes remain in the solution. Also, for doing the calculations we must carefully calculate the values of sines so that we reach an accurate solution.