Question

Solve the system of inequalities graphically: $2x+y\ge 4$, $x+y\le 3$, $2x-3y\le 6$.

Answer 1

Hint: For finding out the region that satisfies the inequalities $2x+y\ge 4$, $x+y\le 3$, $2x-3y\le 6$, we need to find the equality form. This gives the line graph. Change of form of the given equation will give the x-intercept and y-intercept of the lines. We change it to the form of $\dfrac{x}{p}+\dfrac{y}{q}=1$ to find the x intercept, and y intercept of the line as $p$ and $q$ respectively. Then we place the points on the axes and from there we draw the line on the graph. We find the required region based on the origin point’s validity.

Complete step by step solution:
We have to find the x-intercept, and y-intercept of the line $2x+y=4$, $x+y=3$, $2x-3y=6$.
For this we convert the given equation into the form of $\dfrac{x}{p}+\dfrac{y}{q}=1$. From the form we get that the x intercept, and y intercept of the line will be$p$ and $q$ respectively. The points will be $\left( p,0 \right),\left( 0,q \right)$.
The given equation is $2x+y=4$. Converting into the form of $\dfrac{x}{p}+\dfrac{y}{q}=1$, we get
\[\begin{align}
  & 2x+y=4 \\
 & \Rightarrow \dfrac{2x}{4}+\dfrac{y}{4}=1 \\
 & \Rightarrow \dfrac{x}{2}+\dfrac{y}{4}=1 \\
\end{align}\]
Therefore, the x intercept, and y intercept of the line $2x+y=4$ is 2 and 4 respectively. The axes intersecting points are $\left( 2,0 \right),\left( 0,4 \right)$.
The graph of the inequality $2x+y \ge 4$ is shown below.

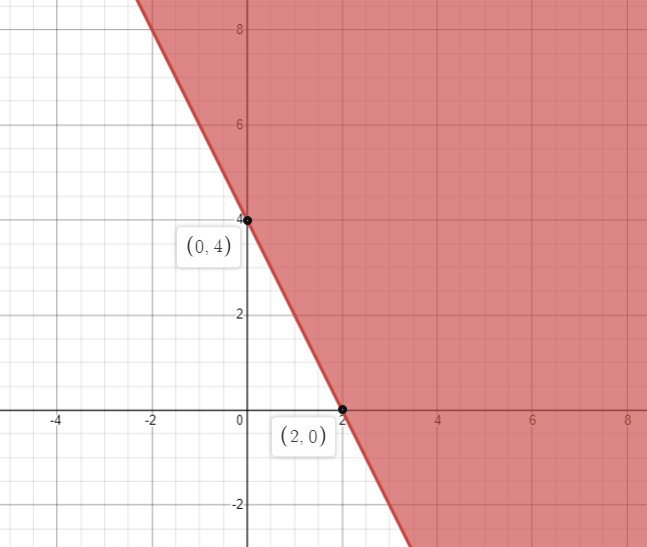
The given equation is $x+y=3$. Converting into the form of $\dfrac{x}{p}+\dfrac{y}{q}=1$, we get
\[\begin{align}
  & x+y=3 \\
 & \Rightarrow \dfrac{x}{3}+\dfrac{y}{3}=1 \\
\end{align}\]
Therefore, the x intercept, and y intercept of the line $x+y=3$ is 3 and 3 respectively. The axes intersecting points are $\left( 3,0 \right),\left( 0,3 \right)$.
The graph of $x+y \le 3$ is shown below.

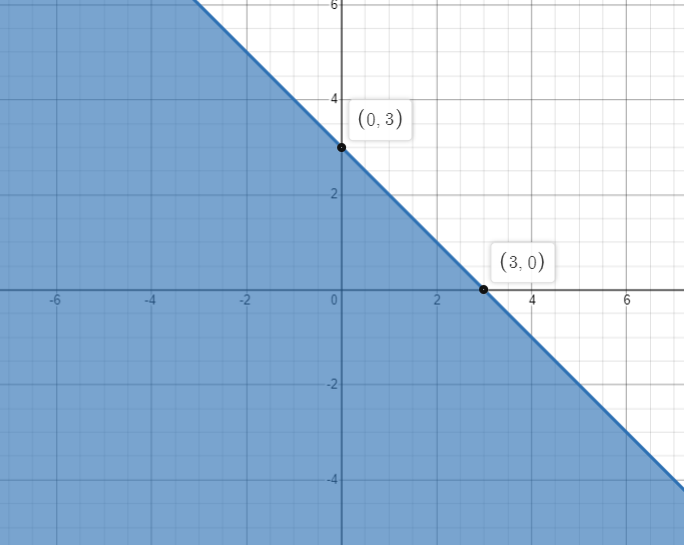
The given equation is $2x-3y=6$. Converting into the form of $\dfrac{x}{p}+\dfrac{y}{q}=1$, we get
\[\begin{align}
  & 2x-3y=6 \\
 & \Rightarrow \dfrac{2x}{6}+\dfrac{\left( -3 \right)y}{6}=1 \\
 & \Rightarrow \dfrac{x}{3}+\dfrac{y}{-2}=1 \\
\end{align}\]
Therefore, the x intercept, and y intercept of the line $2x-3y=6$ is 3 and 2 respectively. The axes intersecting points are $\left( 3,0 \right),\left( 0,-2 \right)$.
The graph of the inequality $2x-3y \le 6$ is shown below

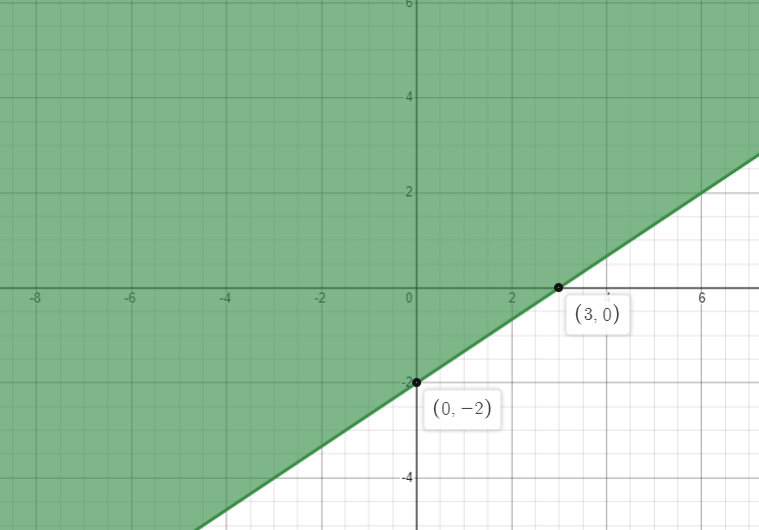
The lines divide the region in two parts. We find the required one based on the credibility of the origin point.

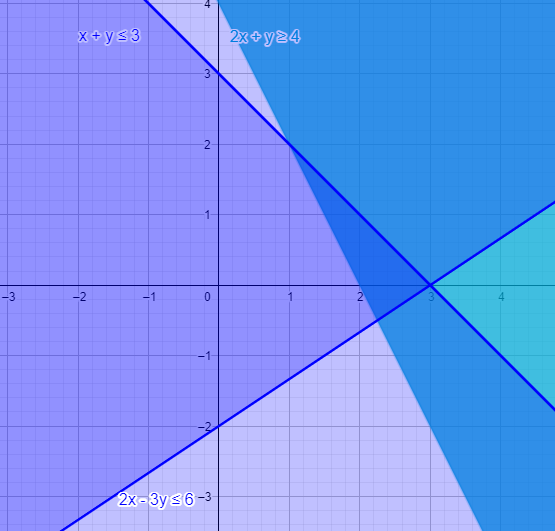
Note:
We take the origin point as that helps in multiplications. We can use any point other than the ones that are on the line itself to find out the required region.
For example, we take the point $\left( -1,-1 \right)$ instead of $\left( 0,0 \right)$.
This means we can take any arbitrary point and that will indicate the area accordingly.