Question

How do you solve the system by graphing: \[y=\dfrac{1}{4}x-1\] and \[y=-2x-10\]?

Answer 1

Hint: Consider the first equation and find the points where it will cut the axes by substituting x = 0 and y = 0 one by one. Similarly, find the points of intersection of the second equation with the two axes. Now, draw the graph of the two equations and observe the point of intersection of the two lines and determine its coordinate to get the answer.

Complete step-by-step solution:
Here, we have been provided with the system of equations: \[y=\dfrac{1}{4}x-1\] and \[y=-2x-10\] and we are asked to solve it using the graph.
Now, let us assume the two equations as: -
\[\Rightarrow y=\dfrac{1}{4}x-1\] - (1)
\[\Rightarrow y=-2x-10\] - (2)
Let us consider equation (1), so we have,
\[\Rightarrow y=\dfrac{1}{4}x-1\]
Substituting x = 0, we get,
\[\Rightarrow y=-1\]
Substituting y = 0, we get,
\[\begin{align}
  & \Rightarrow 0=\dfrac{1}{4}x-1 \\
 & \Rightarrow x=4 \\
\end{align}\]
Therefore, the points where the line will cut the axes are: - A (0, -1) and B (4, 0).
Let us consider equation (2), so we have,
 \[\Rightarrow y=-2x-10\]
Substituting x = 0, we get,
\[\Rightarrow y=-10\]
Substituting y = 0, we get,
\[\Rightarrow -2x-10=0\]
\[\begin{align}
  & \Rightarrow -2x=10 \\
 & \Rightarrow x=-5 \\
\end{align}\]
Therefore, the points where the line will cut the axes are: - C (0, -10) and D (-5, 0).
So, the graph of the two linear equations can be plotted as: -

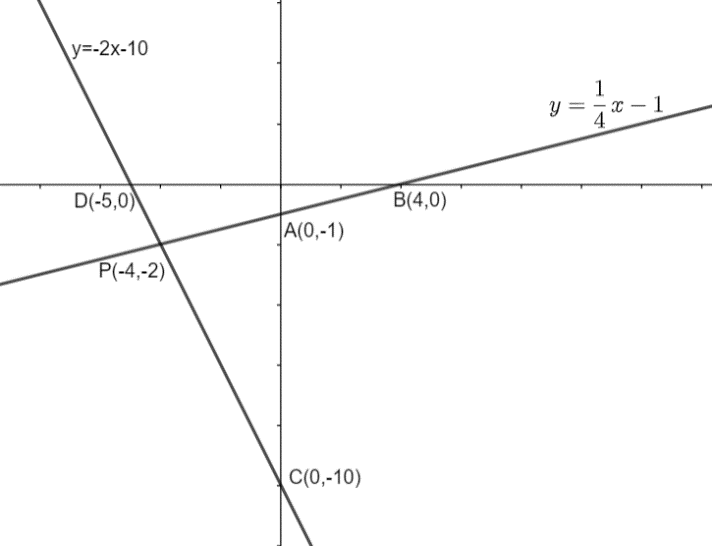
From the above graph we can clearly see that the two straight lines are intersecting at point P whose coordinate is (-4, -2). So, point P (-4, -2) is the solution of the given system of equations.

Note: One may note that we can check our answer by solving the equations of the two given lines algebraically. If we will get the same coordinate of P as in the graph then our answer will be correct. Remember that while drawing the graph, substitute x = 0 and y = 0 to determine the points. If we will use any other values of x and y then we will have to do some calculations to draw the graph. Do not forget to draw and mark important points on the graph like the points where the lines cut the axes.