Question

How do you solve the system by graphing $y = - \dfrac{1}{2}x + 1$ and $y = \dfrac{1}{4}x - 2$?

Answer 1

Hint: we will plot the graph for the equation of lines using intercept form of equation. We will find the intersection points of line on the graph. The intersection point will satisfy the equation of line. We have to find the intercepts of the line on $x - $ axis and $y - $ axis. To find the $y - $ intercept of line, substitute $x = 0$ in the equation of line and substitute $y = 0$ in the equation of line to get $x - $ intercept of the line. We will equate the equation of a given line with the equation of general form of line. The general equation of a line having slope of $m$ and intercepts on the coordinate axis $c$ is $y = mx + c$ . The slopes of a parallel line are equal and if the two lines are parallel then the slope will be equal and they have different $y - $ intercept. A vertical line will have no slope. Slope is defined as the inclination of the line with horizontal axis. Slope is denoted by $m$.

Complete step by step answer:
Step: 1 the given equation of line is $y = - \dfrac{1}{2}x + 1$.
Substitute $x = 0$ in the equation of line to find the $y - $ intercept of the line.
$
   \Rightarrow y = - \dfrac{1}{2} \times 0 + 1 \\
   \Rightarrow y = 1 \\
 $
Therefore the $y - $ intercept of the line is $\left( {0,1} \right)$.
Substitute $y = 0$ in the equation of line to find the $x - $ intercept of the line.
$
   \Rightarrow - \dfrac{1}{2}x + 1 = 0 \\
   \Rightarrow x = 2 \\
 $
Therefore the $x - $ intercept of the line is $\left( {2,0} \right)$.
Step: 2 the given equation of line is $y = \dfrac{1}{4}x - 2$.
Substitute $x = 0$ in the equation of line to find the $y - $ intercept of the line.
$
   \Rightarrow y = \dfrac{1}{4} \times 0 - 2 \\
   \Rightarrow y = - 2 \\
 $
Therefore the $y - $ intercept of the line is $\left( {0, - 2} \right)$.
Substitute $y = 0$ in the equation of line to find the $x - $ intercept of the line.
$
   \Rightarrow \dfrac{1}{4}x - 2 = 0 \\
   \Rightarrow x = 8 \\
 $
Therefore the $x - $ intercept of the line is $\left( {8,0} \right)$.

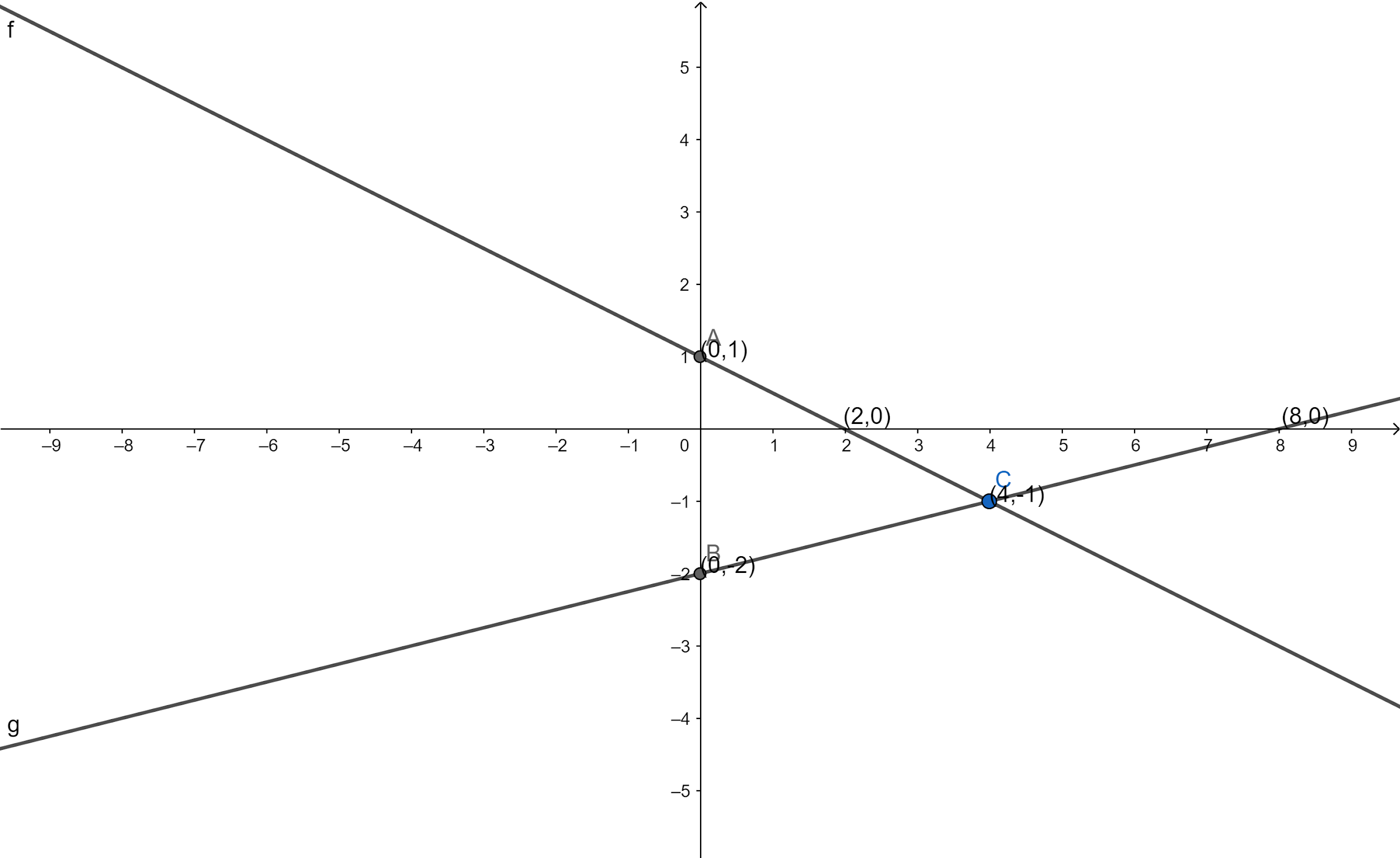
The both lines intersect the graph at a common point C.

Therefore the solution of the system by graph is $x = 4$ and $y = - 1$.

Note: The intersection point of both the lines will be the solution of the system. The common intersection point $\left( {4, - 1} \right)$ of both the lines will satisfy the equation of lines .Plot each equation of line on the graph by finding its intercept made by them on the axis. To find the intercept made by lines on the axis, substitute $x = 0$ and $y = 0$ in the equation of lines