Question

Solve the pair of linear equations by cross - multiplication method.
 $\begin{align}
  & \left( \text{i} \right)2x-5y=4 \\
 & \left( \text{ii} \right)3x-8y=5 \\
\end{align}$

Answer 1

Hint:
In this problem we have to solve the given linear equations by using the method of elimination. In question we observe that they have given a pair of linear equations. The method of elimination involves eliminating the one of the variables from the both the equations. For this we need to have the same variable with the same coefficient in both equations. So, we will first write the coefficients of the variables in both the equations. Now we will consider either one variable and we will multiply both the equations with individual appropriate constants according to coefficients of considered variables. Once we have the same variable with the same coefficient in both the equations, we can do either addition or subtraction of both equations based on the sign of the variable. Now we will simplify the obtained equation to get the required result.

Complete step by step solution:
Given that, pair of the linear equations are
$2x-5y=4$, $3x-8y=5$.
Coefficient of $x$ in the first equation is $2$.
Coefficient of $x$ in the second equation is $3$.
Coefficient of $y$ in the first equations is $-5$.
Coefficient of $y$ in the second equation is $-8$.
Considering the coefficients of $x$. We are going to multiply the first equation with $3$ and the second equation with $2$ to get the coefficients of $x$ in both equations as the same.
Now we will can multiply first equation with $3$ ,then we will get
$\begin{align}
  & 3\left( 2x-5y \right)=3\left( 4 \right) \\
 & \Rightarrow 6x-15y=12....\left( \text{i} \right) \\
\end{align}$
Now we will multiply the second equation with $2$ , then we will have
$\begin{align}
  & 2\left( 3x-8y \right)=2\left( 5 \right) \\
 & \Rightarrow 6x-16y=10.....\left( \text{ii} \right) \\
\end{align}$
We can observe that the coefficients of $x$ in equation $\left( \text{i} \right)$ and $\left( \text{ii} \right)$ are the same. So, we are going to subtract the both the equation, then we will get
$\Rightarrow 6x-15y-\left( 6x-16y \right)=12-10$.
Simplifying the above equation, then we will have
$\begin{align}
  & \Rightarrow 6x-15y-6x+16y=2 \\
 & \Rightarrow y=2 \\
\end{align}$
Substituting the $y$ value in the given first equation, then we will get
$\begin{align}
  & \Rightarrow 2x-5y=4 \\
 & \Rightarrow 2x-5\left( 2 \right)=4 \\
 & \Rightarrow 2x=4+10 \\
 & \Rightarrow 2x=14 \\
 & \Rightarrow x=7 \\
\end{align}$

Hence the solution of the given equations $2x-5y=4$, $3x-8y=5$ is $\left( x,y \right)=\left( 7,2 \right)$.

Note:
We can also plot the graph of the two given equations to get the solution. We will get the graph of the two equations as

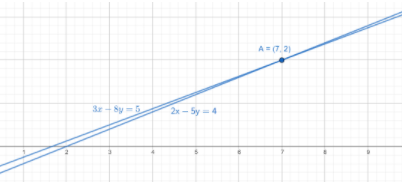
We can also observe the above graph and write the solution of the given equations as $\left( x,y \right)=\left( 7,2 \right)$.