Question

Solve the LPP graphically. Minimize Z = 3x+5y, Subject to constraints
$\begin{align}
  & 2x+3y\ge 12 \\
 & -x+y\le 3 \\
 & x\le 4 \\
 & y\ge 3 \\
\end{align}$

Answer 1

Hint: Let X = 4-x and Y = y-3. Convert the equations of these lines in terms of X and Y. Plot these lines on a graph paper. Recall that the optimum value lies on the corners of the graph formed. Hence find the value of the target function at the corners of the graph and hence determine the minima of the target function.

Complete step-by-step solution -

We have
$\begin{align}
  & 2x+3y=12 \\
 & \Rightarrow 2\left( 4-X \right)+3\left( Y+3 \right)=12 \\
 & \Rightarrow 8-2X+3Y+9=12 \\
 & \Rightarrow -2X+3Y=-5 \\
\end{align}$
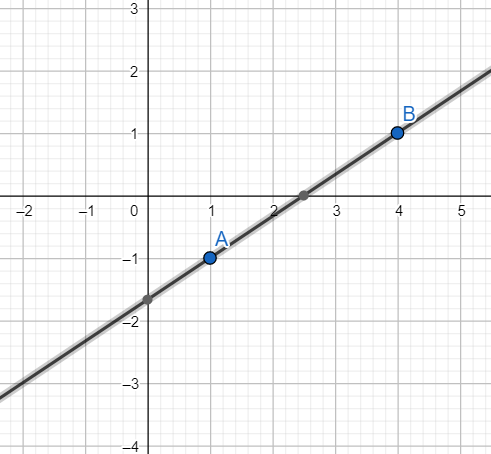
Plotting -2X+3Y = -5 on the graph.
When X = 1, we have
3Y= -3
i.e. $Y=-1$
When Y = 1, we have
-2X = -8
i.e. $X=4$.
Hence two points on the line are $\left( 1,-1 \right)$ and $\left( 4,1 \right)$
Plot these two points on the graph paper and join the points.

We have
$\begin{align}
  & -x+y=3 \\
 & \Rightarrow -\left( 4-X \right)+Y+3=3 \\
 & \Rightarrow -4+X+Y+3=3 \\
 & \Rightarrow X+Y=4 \\
\end{align}$
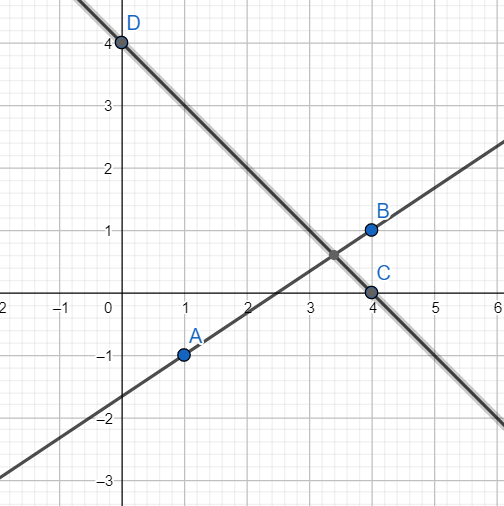
Plotting X+Y = 10.
When X = 0 we have Y = 4.
When Y = 0, we have X= 4
Hence two points on the line are (0,4) and (4,0)
Plot these two points on the graph paper and join the points.

Also
 $\begin{align}
  & x\le 4 \\
 & \Rightarrow x-4\le 0 \\
 & \Rightarrow X\ge 0 \\
\end{align}$
And
$\begin{align}
  & y\ge 3 \\
 & \Rightarrow y-3\ge 0 \\
 & \Rightarrow Y\ge 0 \\
\end{align}$
Now Z = 3x+5y
Hence we have $Z=3\left( 4-X \right)+5\left( Y+3 \right)=-3X+5Y+27$

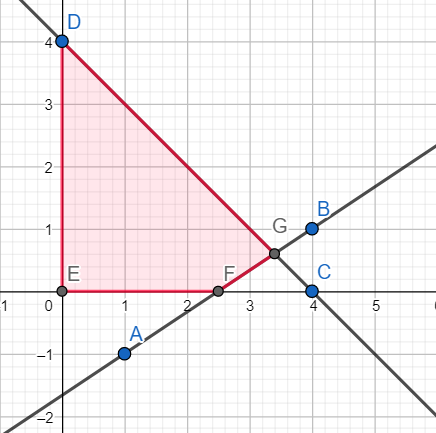
The feasible region is shaded in the above graph.
Finding coordinates of G:
G is the point of intersection of X+Y = 4 and -2X+3Y = -5.
Multiplying X+Y = 4 by 2 and adding to -2X+3y = -5, we get
5Y = 8-5
$\Rightarrow Y=\dfrac{3}{5}=0.6$
Hence Y = 0.6
Hence we have X+(0.6) = 4
Hence we have X = 3.4
Hence coordinates of G are (3.4,0.6).
Finding the coordinates of F:
F is the point of intersection of the X-axis and -2X+3Y = -5
Hence we have Y = 0
Hence -2X=-5
i.e. X = 2.5
Hence the coordinates of F are (2.5,0).
Finding the value of Z at E(0,0):
Z = -3(0)+5(0)+27 = 27.
Finding the value of Z at D(0,4):
Z = -3(0) +5(4)+27 = 47.
Finding the value of Z at G(3.4,0.6):
Z = -3(3.4)+5(0.6)+27 = -10.2+3+27=19.8
Finding the value of Z at F(2.5,0):
Z = -3(2.5)+5(0)+27 = 19.5
Hence the minimum value of Z is 19.5 at X = 2.5 and Y = 0
x =4-X
Hence x = 1.5
y = Y+3 = 3.
Hence the minimum value of Z is 19.5, which occurs at x=1.5 and y = 3.

Note: [1] Conversion of the given equations in $X\ge 0$ and $Y\ge 0$ is not necessary. However, it is a standard procedure while solving LP problems.
[2] You can also apply the simplex method to find the minima of the above problem.
The simplex method is an algorithmic process of finding the optima of Linear programming problems.
[3] In the above solution one can note that $x\le 4$ and $2x+3y\ge 12$ were sufficient to determine the minima. This is known as complementary slackness.