Question

How do you solve the inequality $\dfrac{x}{3} + 5 \leqslant 14$?

Answer 1

Hint: First, obtain the linear inequation. Then, collect all terms involving the variable on one side of the inequation and the constant terms on the other side and simplify both sides of inequality in their simplest forms to reduce the inequation in the form $ax \leqslant b$. Then, solve the inequation obtained by dividing both sides of the inequation by the coefficient of the variable. Finally, write the solution set obtained in the form of an interval on the real line.
Formula used:
In the process of solving an inequation, we use mathematical simplifications which are governed by the following rules:
Rule 1 Same number may be added to (or subtracted from) both sides of an inequation without changing the sign of inequality.
Rule 2 Both sides of an inequation can be multiplied (or divided) by the same positive real number without changing the sign of inequality. However, the sign of inequality is reversed when both sides of an inequation are multiplied or divided by a negative number.
Rule 3 Any term of an inequation may be taken to the other side with its sign changed without affecting the sign of inequality.

Complete step by step answer:
The given inequation is
$\dfrac{x}{3} + 5 \leqslant 14$…(i)
We have to solve this inequality, i.e., find the solution set for $x$.
Collect all terms involving the variable on one side of the inequation and the constant terms on the other side and simplify both sides of inequality in their simplest forms to reduce the inequation in the form $ax \leqslant b$.
For this, subtract $5$ from both sides of inequation (i).
So, by rule 1, $\dfrac{x}{3} \leqslant 9$…(ii)
Solve the inequation (ii) by dividing both sides of the inequation by the coefficient of the variable.
For this, multiply both sides of inequation (ii) by $3$.
So, by rule 2, $x \leqslant 27$
Hence, any real number less than or equal to $27$ is a solution of inequation (i).
These solutions can be graphed on real line as shown below:

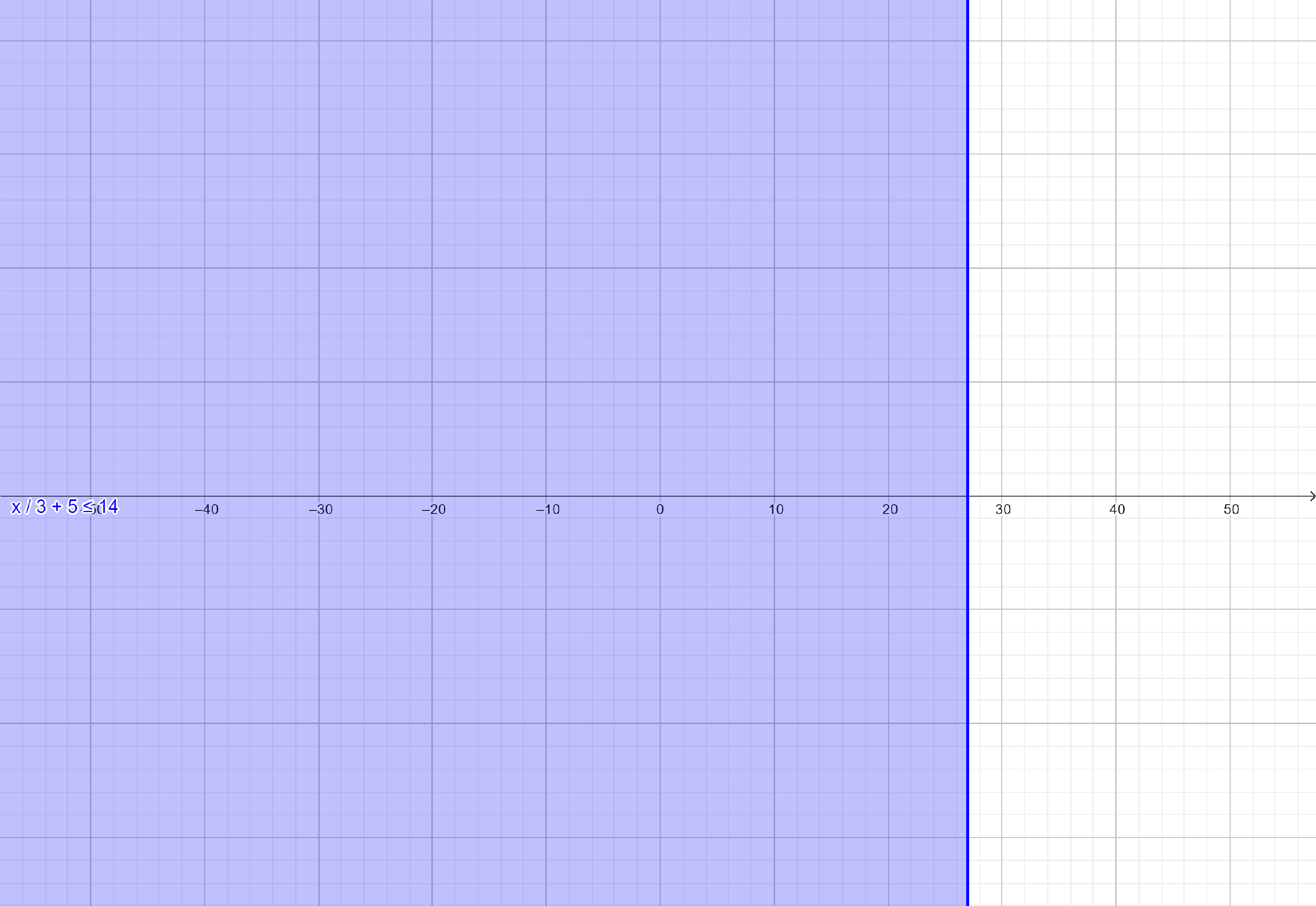
The solution set of inequation (i) is $\left( { - \infty ,27} \right]$.
Final solution: Thus, the solution set of the given inequation is $\left( { - \infty ,27} \right]$.

Note:
We follow the following algorithm to solve a linear inequation in one variable.
Algorithm:
Step I Obtain the linear inequation.
Step II Collect all terms involving the variable on one side of the inequation and the constant terms on the other side.
Step III Simplify both sides of inequality in their simplest forms to reduce the inequation in the form $ax < b$, or $ax \leqslant b$, or $ax > b$, or $ax \geqslant b$
Step IV Solve the inequation obtained in step III by dividing both sides of the inequation by the coefficient of the variable.
Step V Write the solution set obtained in step IV in the form of an interval on the real line.