Question

Solve the inequality \[ - 3 \leqslant 3 - 2x < 9,x \in R.\] represent the solution on a number line.

Answer 1

Hint: To solve this type of inequality first divide this inequality into two parts: left inequality and right inequality. After splitting into two try to solve in terms of \[x\] only. And then try to represent those points on a number line and apply the conditions to all and try to find the intersection of both the inequalities.

Complete step-by-step solution:
Given,
\[ - 3 \leqslant 3 - 2x < 9,x \in R.\]
So let's divide the inequality into two parts
\[ - 3 \leqslant 3 - 2x < 9 = 3 - 2x \geqslant - 3\,and\,3 - 2x < 9\]
Inequality (i) is
\[3 - 2x \geqslant - 3\] ………...……(i)
Inequality (ii) is
\[\,3 - 2x < 9\] ………………………(ii)
Solving inequation (i)
\[3 - 2x \geqslant - 3\]
On further arranging
\[ - 2x \geqslant - 3 - 3\]
\[ \Rightarrow - 2x \geqslant - 6\]
On multiplying by \[ - \] the inequality will change from greater then to less then
\[2x \leqslant 6\]
\[\Rightarrow x \leqslant 3\] …………………………………(iii)
Now solving inequality (ii)
\[\,3 - 2x < 9\]
\[\Rightarrow \, - 2x < 9 - 3\]
\[\Rightarrow \, - 2x < 6\]
On multiplying by \[ - \] the inequality will change from greater then to less then
\[\,2x > - 6\]
\[\Rightarrow \,x > \dfrac{{ - 6}}{2}\]
\[\Rightarrow \,x > - 3\] ……………………(iv)
Equation (iii) says that \[x\] is less than or equal to \[3\] and equation (iv) says that \[x\] is greater than \[ - 3\].
On applying the condition of equation (iii) and (iv) on the number line look like the given fig.

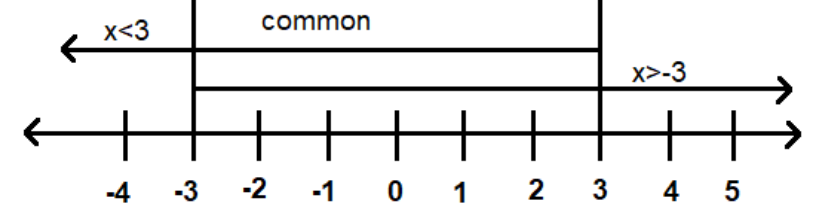
Solution of the given equation is \[ - 3 < x \leqslant 3\]. If \[x\] is out of this range then the inequality does not hold good. If we put the value of \[x\] out of range in the main inequality then some unexpected answers are coming that are not accepted by mathematics.

Note: To solve this type of question you must know the knowledge of inequality and how we represent that inequality in one number line. Take a look while multiplying with the \[ - \] sign because if you multiply by the \[ - \] sign then inequality will change from greater then to less than. At last, we have to take the intersection of both the inequalities.