Question

Solve the given trigonometric expression $\dfrac{\text{cos4}{{\text{5}}^{\circ }}}{\sec {{30}^{\circ }}+\cos ec{{30}^{\circ }}}$ .

Answer 1

Hint: Using trigonometric standard angles table write the expression in the value and then further rationalize it to get the answer.

Complete step-by-step solution -
 In the question we are given on expression which is $\dfrac{\text{cos4}{{\text{5}}^{\circ }}}{\sec {{30}^{\circ }}+\cos ec{{30}^{\circ }}}$ and we have to evaluate or find the value of it.
We are given the expression which is,
 $\dfrac{\text{cos4}{{\text{5}}^{\circ }}}{\sec {{30}^{\circ }}+\cos ec{{30}^{\circ }}}$ .
As we can see that the angles whose trigonometric ratios are given are standard angles.
Generally, the values of trigonometric standard angles are generally written as trigonometric standard angles tables.
The table is shown below:

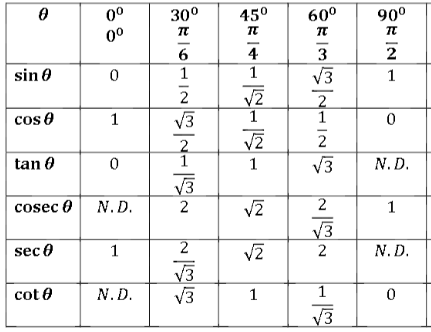
For the expression we only want values of some of the trigonometric standard angles only like according to the question we want values of $\cos {{45}^{\circ }},\sec {{30}^{\circ }}$and $\cos ec{{30}^{\circ }}$.
So from the standard angles table we can see that value of $\cos {{45}^{\circ }}$ is $\dfrac{1}{\sqrt{2}}$ , $\sec {{30}^{\circ }}$ is $\dfrac{2}{\sqrt{3}}$ and $\cos ec{{30}^{\circ }}$ is 2 .
 So on substituting we get ,
$\dfrac{\dfrac{1}{\sqrt{2}}}{\dfrac{2}{\sqrt{3}}+2}$ .
Now we will multiply by $2\sqrt{3}$ to both numerator and denominator we get,
$\dfrac{\dfrac{1}{\sqrt{2}}\times 2\sqrt{3}}{\dfrac{2}{\sqrt{3}}+2\sqrt{3}+2\times 2\sqrt{3}}$.
On simplification we get,
 $\dfrac{\sqrt{6}}{\text{4+4}\sqrt{3}}=\dfrac{\sqrt{6}}{\text{4}\left( \sqrt{3}+1 \right)}$ .
Now, we will rationalize the function by multiplying with $\left( \sqrt{3}-1 \right)$ to both numerator and denominator we get ,
$\dfrac{\sqrt{6}}{\text{4}\left( \sqrt{3}+1 \right)}\times \dfrac{\sqrt{3}-1}{\sqrt{3}-1}$ .
Now, on multiplication and simplification we get,
 $\dfrac{\sqrt{6}\left( \sqrt{3}-1 \right)}{\text{4}\times \left( 3-1 \right)}=\dfrac{\sqrt{6}.\left( \sqrt{3}-1 \right)}{\text{8}}$ .
Hence, the answer is $\dfrac{\sqrt{6}\left( \sqrt{3}-1 \right)}{8}$ .

Note: While doing rationalization if the fraction is in form of $\dfrac{\text{c}}{\text{a+}\sqrt{b}}$ then we can rationalize it by multiplying numerator and denominator $a-\sqrt{b}$ and simplify it further. By rationalization In denominator we try to remove radicals.