Question

Solve the following systems of equations graphically:
x + y = 3
2x + 5y = 12

Answer 1

Hint: For system of equations the solution follow some conditions
If there are system of equations, namely $ax+by+c=0$ and $dx+ey+f=0$
Then, $\begin{align}
  & \dfrac{a}{d}=\dfrac{b}{e}=\dfrac{c}{f}\Rightarrow Infinite\text{ }solutions \\
 & \dfrac{a}{d}=\dfrac{b}{e}\ne \dfrac{c}{f}\Rightarrow No\text{ }solutions \\
\end{align}$

Complete step-by-step answer:
Definition of system of equations:
If simultaneously we have more than one equation, then the set of those equations is called a system of equations. We can project systems of equations as lines, planes etc. depending on number of variables.
If we have 2 variables:
Then system of equations is analogous to straight lines
If we have 3 variables:
Then the system of equations is analogous to the planes.
Here we have 2 variables. So in our case:
Our system of equations is analogous to 2 straight lines.
We have 3 possibilities
(a) No Solutions
(b) Infinite solutions
(c) 1 solution.

(a) No solution:
If two straight lines (infinitely long) have 0 solutions then they must not intersect anywhere that means they are parallel lines.
For 2 lines to be parallel their x – coordinates and y – coordinates must be proportional but constant must not be in proportion to them.
In mathematical way:
If system of equations are
$ax+by+c=0$ $dx+ey+f=0$
then $\begin{align}
  & \dfrac{a}{d}=\dfrac{b}{e}\ne \dfrac{c}{f} \\
 & \Rightarrow No\text{ }Solutions \\
\end{align}$
(b) Infinite solutions
If 2 infinitely long straight lines have infinite solutions then they must be coincident lines, as infinite intersection points implies infinite solutions their x-coordinates, y-coordinates and constants must be in proportion
In mathematical way:
If system of equations are
$\begin{align}
  & ax+by+c=0 \\
 & dx+ey+f=0 \\
\end{align}$
Then $\begin{align}
  & \dfrac{a}{d}=\dfrac{b}{e}=\dfrac{c}{f} \\
 & \Rightarrow Infinite\text{ }Solutions \\
\end{align}$
(c) 1 solution:
If 2 infinitely long straight lines have 1 solution they must be intersecting at only one 1 point.
$\Rightarrow $ If not the above 2 cases then the system of equations satisfy this case.
Given equations are: $x+y=3;$ $2x+5y=12$
By system of equations: $a=1,b=1,c=-3,d=2,e=5,f=-12$
$\dfrac{a}{d}=\dfrac{1}{2};\dfrac{b}{e}=\dfrac{1}{5}$ \[\dfrac{a}{d}\ne \dfrac{b}{e}\Rightarrow \] Intersecting lines
We need 4 points for plot
By substituting $y=0$ in 1st line, we get $x=3$
By substituting $x=0$ in 1st line, we get $y=3$
By substituting $y=0$ in 2nd line, we get $x=6$
By substituting $x=0$ in 2nd line, we get $5y=12\Rightarrow y=2.4$

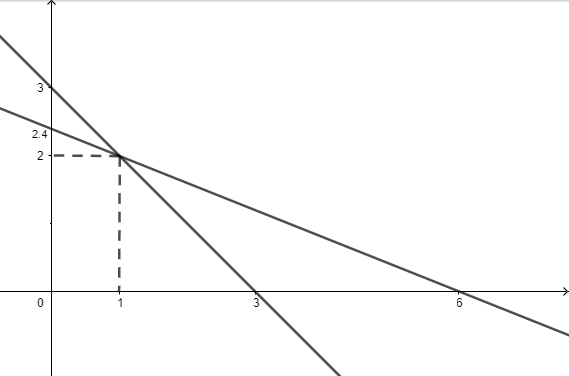
$\Rightarrow $ By system of equation also we got intersecting lines so, graph is correct
By graph, we can see that $x$ - coordinate of intersection is 1.
By graph, we can see that $y$ - coordinate of intersection is 2.
So, point of intersection is by (1, 2)
Hence this is the solution of the equation.
Therefore, we solved using graphs.

Note: Be careful while assigning points to the line we solved equations by system of equations first, to just check whether our graphical representation is correct or not. We must do it or else we might not know if the graph is correct or not.