Question

Solve the following system of equations by substitution method.
$\begin{align}
  & x+y=7 \\
 & 3x-2y=11 \\
\end{align}$

Answer 1

Hint: In the substitution method, we express one variable in terms of the other variable in one equation and substitute that value in the next equation to get a linear equation in one variable only. We then solve the linear equation and substitute the value in one equation to get the value of the other variable.

Complete step-by-step answer:

We have the following system of equations
$\begin{align}
  & x+y=7\text{ (i)} \\
 & 3x-2y=11\text{ (ii)} \\
\end{align}$
From equation (i) we have $x+y=7$
Subtracting y from both sides of the equation, we get
$\begin{align}
  & x+y-y=7-y \\
 & \Rightarrow x=7-y\text{ (iii)} \\
\end{align}$
Substituting the value of x from equation (iii) in equation (ii), we get
$\begin{align}
  & 3\left( 7-y \right)-2y=11 \\
 & \Rightarrow 21-3y-2y=11 \\
 & \Rightarrow 21-5y=11 \\
\end{align}$
Adding 5y on both sides, we get
$\begin{align}
  & 21-5y+5y=11+5y \\
 & \Rightarrow 11+5y=21 \\
\end{align}$
Subtracting 11 from both sides, we get
$\begin{align}
  & 11+5y-11=21-11 \\
 & \Rightarrow 5y=10 \\
\end{align}$
Dividing by 5 on both sides, we get
$\begin{align}
  & \dfrac{5y}{5}=\dfrac{10}{5} \\
 & \Rightarrow y=2 \\
\end{align}$
Substituting the value of y in equation (iii) we get
$x=7-y=7-2=5$
Hence x = 2, y=5 is the solution of the given system of equations.

Note: [1] We can also solve the above question by using the Matrix method.
In matrix method we write the given system of equations as AX=B
Pre-multiplying both sides by ${{A}^{-1}}$ we get
$\begin{align}
  & {{A}^{-1}}AX={{A}^{-1}}B \\
 & \Rightarrow IX={{A}^{-1}}B \\
 & \Rightarrow X={{A}^{-1}}B \\
\end{align}$
Hence the solutions are found.
In the given question we have $A=\left[ \begin{matrix}
   1 & 1 \\
   3 & -2 \\
\end{matrix} \right]$, $X=\left[ \begin{matrix}
   x \\
   y \\
\end{matrix} \right]$ and $B=\left[ \begin{matrix}
   7 \\
   11 \\
\end{matrix} \right]$
Finding the inverse:
We know ${{A}^{-1}}=\dfrac{1}{\det (A)}adj(A)$
$\begin{align}
  & \det (A)=1(-2)-3(1)=-2-3=-5 \\
 & adj(A)={{\left[ \begin{matrix}
   -2 & -3 \\
   -1 & 1 \\
\end{matrix} \right]}^{T}}=\left[ \begin{matrix}
   -2 & -1 \\
   -3 & 1 \\
\end{matrix} \right] \\
\end{align}$
Hence, we have ${{A}^{-1}}=\dfrac{1}{-5}\left[ \begin{matrix}
   -2 & -1 \\
   -3 & 1 \\
\end{matrix} \right]$
i.e. ${{A}^{-1}}=\left[ \begin{matrix}
   \dfrac{2}{5} & \dfrac{1}{5} \\
   \dfrac{3}{5} & \dfrac{-1}{5} \\
\end{matrix} \right]$
Hence, we have $X={{A}^{-1}}B=\left[ \begin{matrix}
   \dfrac{2}{5} & \dfrac{1}{5} \\
   \dfrac{3}{5} & \dfrac{-1}{5} \\
\end{matrix} \right]\times \left[ \begin{matrix}
   7 \\
   11 \\
\end{matrix} \right]=\left[ \begin{matrix}
   \dfrac{14}{5}+\dfrac{11}{5} \\
   \dfrac{21}{5}-\dfrac{11}{5} \\
\end{matrix} \right]=\left[ \begin{matrix}
   \dfrac{25}{5} \\
   \dfrac{10}{5} \\
\end{matrix} \right]=\left[ \begin{matrix}
   5 \\
   2 \\
\end{matrix} \right]$
Hence x =5 and y = 2 is the solution of the given system of equations.
[2] Graphically we can find the coordinates of the point of intersection of these lines to get the solution of the system of equations.

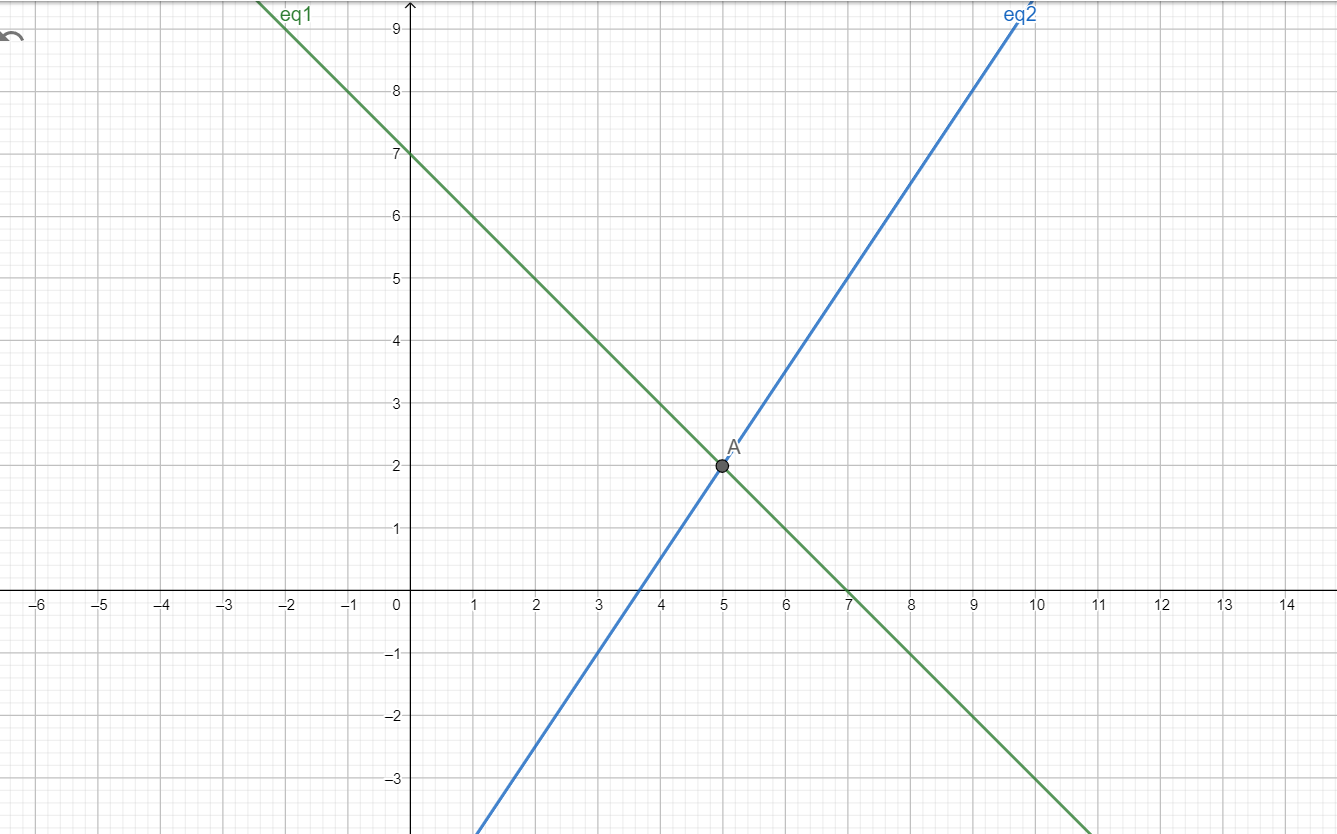
As is evident from the graph the two lines intersect at point A (5,2)
Hence x = 5 and y = 2 is the solution of the given system of equations.