
Solve the following simultaneous equations using Graphical method:
x + 2y = 5
y = – 2x – 2
Then (x, y) is equal to
(a) (– 3, 4)
(b) (4, – 2)
(c) (3, 4)
(d) (4, 2)
Answer
617.1k+ views
Hint: In this question, first of all, get the two points passing from each line and draw the lines in the xy plane. Substitute x and y equal to 0 to get these points or any number of your choice. Now, properly see from the graph the point of intersection of these lines which would be the solution of the equations.
Complete step-by-step answer:
In this question, we have to solve the following system of equations graphically.
\[x+2y=5....\left( i \right)\]
\[y+2x=-2....\left( ii \right)\]
In this question, first of all, we will plot two lines and then check their point of intersection by checking the meeting point of lines on the graph. We know that to plot a line, we need at least 2 points. So, by substituting x = 0 in equation (i), we get,
\[x+2y=5\]
\[0+2y=5\]
\[y=\dfrac{5}{2}\]
So, we get, x = 0 and \[y=\dfrac{5}{2}\]
Now, let us substitute y = 0 in equation (i), we get,
\[x+2y=5\]
\[x+2\left( 0 \right)=5\]
\[x=5\]
So, we get, x = 5 and y = 0.
So, for this line, we get,
By plotting these points in the graph, we get,
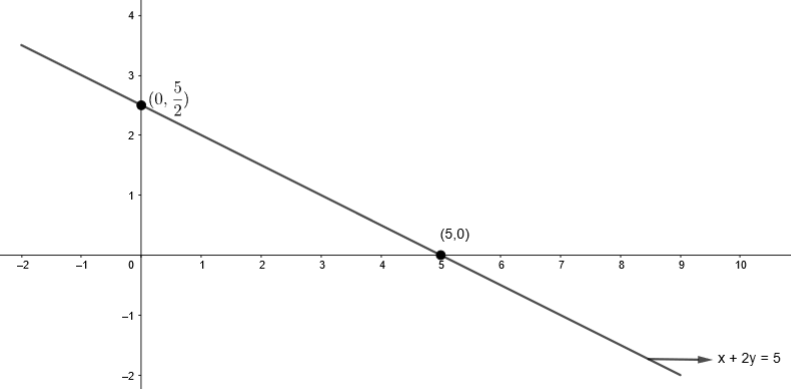
Similarly, by substituting x = 0 in equation (ii), we get,
\[y+2x=-2\]
\[y+2\left( 0 \right)=-2\]
\[y=-2\]
So, we get, x = 0 and y = – 2.
Now, by substituting y = 0 in equation (ii), we get,
\[y+2x=-2\]
\[0+2x=-2\]
\[x=\dfrac{-2}{2}\]
\[x=-1\]
So, we get, x = – 1 and y = 0
So, for this line, we get,
By plotting these points in the graph, we get,
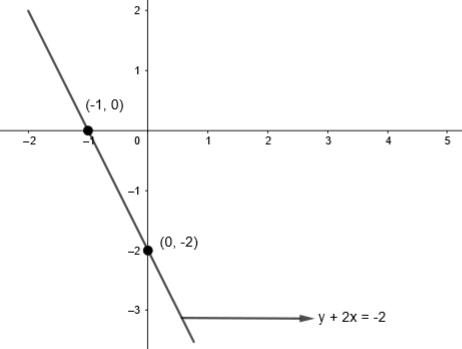
Now, we will draw both the lines in one graph, we get,
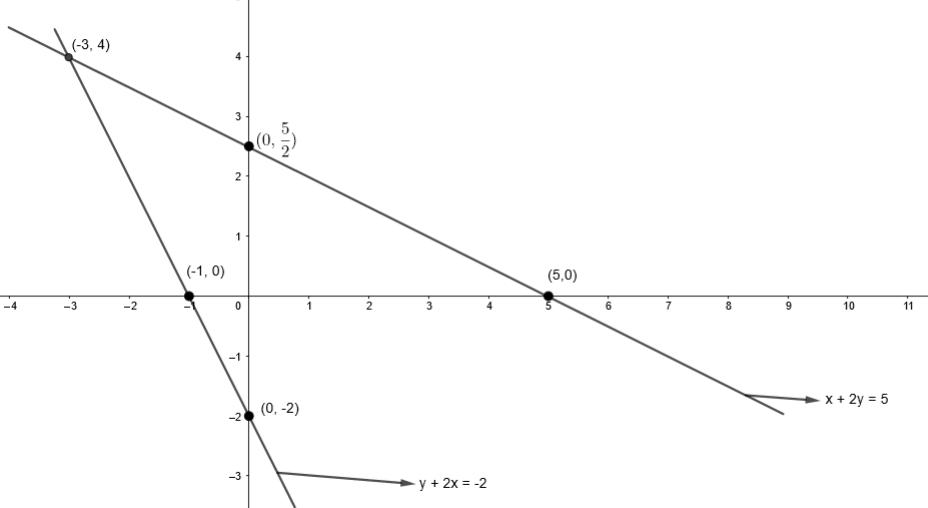
So, from the graph, we get the solution or intersection of lines as (x, y) = (– 3, 4).
Hence, option (a) is the right answer.
Note: In this question, it is very important to take the scale while drawing both the lines of each set as the same because then only we will get the correct point of intersection. Also, students should cross-check their answer by substituting the point of intersection in both the equations of the set by checking if these values of x and y are satisfying them or not.
Complete step-by-step answer:
In this question, we have to solve the following system of equations graphically.
\[x+2y=5....\left( i \right)\]
\[y+2x=-2....\left( ii \right)\]
In this question, first of all, we will plot two lines and then check their point of intersection by checking the meeting point of lines on the graph. We know that to plot a line, we need at least 2 points. So, by substituting x = 0 in equation (i), we get,
\[x+2y=5\]
\[0+2y=5\]
\[y=\dfrac{5}{2}\]
So, we get, x = 0 and \[y=\dfrac{5}{2}\]
Now, let us substitute y = 0 in equation (i), we get,
\[x+2y=5\]
\[x+2\left( 0 \right)=5\]
\[x=5\]
So, we get, x = 5 and y = 0.
So, for this line, we get,
| x | 0 | 5 |
| y | \[\dfrac{5}{2}\] | 0 |
By plotting these points in the graph, we get,

Similarly, by substituting x = 0 in equation (ii), we get,
\[y+2x=-2\]
\[y+2\left( 0 \right)=-2\]
\[y=-2\]
So, we get, x = 0 and y = – 2.
Now, by substituting y = 0 in equation (ii), we get,
\[y+2x=-2\]
\[0+2x=-2\]
\[x=\dfrac{-2}{2}\]
\[x=-1\]
So, we get, x = – 1 and y = 0
So, for this line, we get,
| x | 0 | -1 |
| Y | -2 | 0 |
By plotting these points in the graph, we get,

Now, we will draw both the lines in one graph, we get,

So, from the graph, we get the solution or intersection of lines as (x, y) = (– 3, 4).
Hence, option (a) is the right answer.
Note: In this question, it is very important to take the scale while drawing both the lines of each set as the same because then only we will get the correct point of intersection. Also, students should cross-check their answer by substituting the point of intersection in both the equations of the set by checking if these values of x and y are satisfying them or not.
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
Which country won the ICC Men's ODI World Cup in 2023?

In cricket, how many legal balls are there in a standard over?

Explain the Treaty of Vienna of 1815 class 10 social science CBSE

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

What does "powerplay" mean in limited-overs cricket?

What is the "Powerplay" in T20 cricket?




