
Solve the following pair of linear equations by cross multiplication method $2x+y=5,3x+2y=8$ .
Answer
604.5k+ views
- Hint: First look at the definition of Cross multiplication method carefully. Find the variables a, b, c, d, e, f from the equations given in the question. You must find variables by comparing given equations with $ax+by+c=0$ ; $dx+ey+f=0$. Now, use the relation between x, y and these assumed variables a, b, c, d, e, f and find the values of x, y. By formula equation you can get the variables x, y in terms of the newly assumed variables. Cross multiplication method equation:
$\dfrac{x}{bf-ec}=\dfrac{y}{cd-fa}=\dfrac{1}{ae-db}$
Complete step-by-step solution -
Cross Multiplication Method: In mathematics, cross multiplication method means we multiply the numerator of each side by the denominator of the other side, effectively crossing the terms over.
We write x, y, a, b, c, d, e, f as follows to get the formula: - Use cross multiplying after this to get x, y.
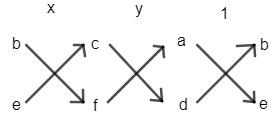
$\dfrac{x}{bf-ec}=\dfrac{y}{cd-fa}=\dfrac{1}{ae-db}$
By cross multiplication at first and last term, we get value of x:
$x=\dfrac{bf-ec}{ae-db}$ ………………………………………..(i)
By cross multiplying at second and last term, we get value of y:
$y=\dfrac{cd-fa}{ae-db}$ ………………………………………(ii)
Given equations in the question, are written in the form of:
$2x+y=5,3x+2y=8$
By comparing these equations with $ax+by+c=0$ , $dx+ey+f=0$ we get variables as:
$a=2,b=1,c=-5,d=3,e=2,f=-8$
By substituting these values in equation (i), we get x as:
$x=\dfrac{\left( -8 \right)-\left( -10 \right)}{\left( 4 \right)-\left( 3 \right)}$
By simplifying, we get value of x as a constant: $x=2$
By substituting a, b, c, d, e, f in equation (ii), we get y as:
$y=\dfrac{\left( -15 \right)-\left( -16 \right)}{\left( 4 \right)-\left( 3 \right)}$
By simplifying the above equation, we get value of y as: \[y=1\]
Therefore, \[\left( 2,1 \right)\] is the solution of given equations.
Note: In cross multiplication method the representation is very crucial. Generally, students confuse and write a in place of b and vice-versa which will lead to wrong answers. Be careful while comparing you must make the right hand side zero. Generally, students take the constant as c but you must make sure the constant must be on the left hand side or else you will miss a negative sign and lead to the wrong answer.
$\dfrac{x}{bf-ec}=\dfrac{y}{cd-fa}=\dfrac{1}{ae-db}$
Complete step-by-step solution -
Cross Multiplication Method: In mathematics, cross multiplication method means we multiply the numerator of each side by the denominator of the other side, effectively crossing the terms over.
We write x, y, a, b, c, d, e, f as follows to get the formula: - Use cross multiplying after this to get x, y.
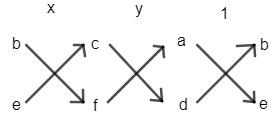
$\dfrac{x}{bf-ec}=\dfrac{y}{cd-fa}=\dfrac{1}{ae-db}$
By cross multiplication at first and last term, we get value of x:
$x=\dfrac{bf-ec}{ae-db}$ ………………………………………..(i)
By cross multiplying at second and last term, we get value of y:
$y=\dfrac{cd-fa}{ae-db}$ ………………………………………(ii)
Given equations in the question, are written in the form of:
$2x+y=5,3x+2y=8$
By comparing these equations with $ax+by+c=0$ , $dx+ey+f=0$ we get variables as:
$a=2,b=1,c=-5,d=3,e=2,f=-8$
By substituting these values in equation (i), we get x as:
$x=\dfrac{\left( -8 \right)-\left( -10 \right)}{\left( 4 \right)-\left( 3 \right)}$
By simplifying, we get value of x as a constant: $x=2$
By substituting a, b, c, d, e, f in equation (ii), we get y as:
$y=\dfrac{\left( -15 \right)-\left( -16 \right)}{\left( 4 \right)-\left( 3 \right)}$
By simplifying the above equation, we get value of y as: \[y=1\]
Therefore, \[\left( 2,1 \right)\] is the solution of given equations.
Note: In cross multiplication method the representation is very crucial. Generally, students confuse and write a in place of b and vice-versa which will lead to wrong answers. Be careful while comparing you must make the right hand side zero. Generally, students take the constant as c but you must make sure the constant must be on the left hand side or else you will miss a negative sign and lead to the wrong answer.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




