Question

Solve the following linear equation in R:
$\dfrac{x}{x-5}>\dfrac{1}{2}$

Answer 1

Hint: We have given an inequality as follows: $\dfrac{x}{x-5}>\dfrac{1}{2}$. Now, subtract $\dfrac{1}{2}$ on both the sides of the given equation then solve the subtraction and then find the solutions in x such that the solutions of x are satisfying this inequality. While considering the solutions of x, make sure you will exclude the solution when x is 5 because when x is 5 then the denominator becomes 0 and we know that when the denominator is 0 then the solution becomes not defined.

Complete step-by-step answer:
We have given the following inequality:
$\dfrac{x}{x-5}>\dfrac{1}{2}$
We have to solve this inequality and find the values of x.
Now, subtracting $\dfrac{1}{2}$ on both the sides of this inequality which will give us:
$\dfrac{x}{x-5}-\dfrac{1}{2}>0$
Taking 2 and $\left( x-5 \right)$ as L.C.M on the L.H.S of the above equation we get,
$\begin{align}
  & \dfrac{2x-\left( x-5 \right)}{2\left( x-5 \right)}>0 \\
 & \Rightarrow \dfrac{x+5}{2\left( x-5 \right)}>0 \\
\end{align}$
The critical points of the above inequality are:
When $\left( x+5=0 \right)\And \left( x-5=0 \right)$ so solving these inequalities we get,
$\begin{align}
  & x+5=0 \\
 & \Rightarrow x=-5 \\
 & x-5=0 \\
 & \Rightarrow x=5 \\
\end{align}$
Now, we got the critical points as -5, 5.
Plotting these points on the number line we get,

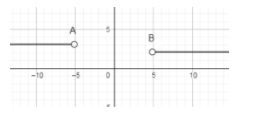
Now, if we substitute the values which are greater than 5 then the expression becomes positive because both $\left( x+5 \right)\And \left( x-5 \right)$ becomes positive. And if we put values which are less than -5 then also we will get the whole term positive because $\left( x+5 \right)\And \left( x-5 \right)$ both becomes negative and division of two negative terms is positive.
Hence, the range of values of x where the given expression holds true is:
$x\in \left( -\infty ,-5 \right)\bigcup \left( 5,\infty \right)$
In the above expression, $\left( -\infty ,-5 \right)$ means the x can take values less than -5 and $\left( 5,\infty \right)$ means that the x can take values greater than 5. And $\bigcup $ means union of the two ranges of x that we have just shown.

Note: The point to be noted here is that in the range of values of x that we have written above, don’t include the critical points 5 and -5. There are two reasons for that:
First is if x equals 5 then the denominator becomes 0 and the solution becomes not defined and the other reason is that we have given the inequality “>” not an equality so we cannot include the values.
For e.g. if instead of inequality “>” $''\ge ''$ sign is given then the expression becomes:
$\dfrac{x+5}{2\left( x-5 \right)}\ge 0$
Then we are going to include -5 also but again, we are not including 5 because then the solution becomes not defined. Then the range of solutions for the above inequality is:
\[x\in (-\infty ,-5]\bigcup \left( 5,\infty \right)\]