Question

Solve the following inequality, \[{{\log }_{0.2}}\left( {{x}^{2}}-x-2 \right)>{{\log }_{0.2}}\left( -{{x}^{2}}+2x+3 \right)\] .

Answer 1

Hint: The terms inside the log can never be negative. So, \[\left( {{x}^{2}}-x-2 \right)>0\] and \[\left( -{{x}^{2}}+2x+3 \right)>0\] . Now, solve these two equations and get the range of values of x. Now, remove the log from the expression \[{{\log }_{0.2}}\left( {{x}^{2}}-x-2 \right)>{{\log }_{0.2}}\left( -{{x}^{2}}+2x+3 \right)\] by using the property that inequality sign reverses while removing the log if the base of the logarithm is less than 1. Now, solve \[\left( {{x}^{2}}-x-2 \right)<\left( -{{x}^{2}}+2x+3 \right)\] and get the values of x. Finally, take the intersection of all the range of values of x.

Complete step-by-step answer:

According to the question, our given inequality is,
\[{{\log }_{0.2}}\left( {{x}^{2}}-x-2 \right)>{{\log }_{0.2}}\left( -{{x}^{2}}+2x+3 \right)\] …………………(1)
We know the property that the term inside the ‘log’ can never be negative.
Using this property, we can say that \[\left( {{x}^{2}}-x-2 \right)\] and \[\left( -{{x}^{2}}+2x+3 \right)\] are greater than 0.
\[\left( {{x}^{2}}-x-2 \right)>0\] ……………(2)
\[\left( -{{x}^{2}}+2x+3 \right)>0\] ………………..(3)
Solving equation (2), we get
\[\left( {{x}^{2}}-x-2 \right)>0\]
Factorising the expression, we get
\[\begin{align}
  & \left( {{x}^{2}}-2x+x-2 \right)>0 \\
 & x(x-2)+1(x-2)>0 \\
 & (x+1)(x-2)>0 \\
\end{align}\]
So, \[x<-1\] and \[x>2\] ……………..(4)
Solving equation (2), we get
\[\left( -{{x}^{2}}+2x+3 \right)>0\]
Factorising the expression, we get
\[\begin{align}
  & \left( -{{x}^{2}}+2x+3 \right)>0 \\
 & -{{x}^{2}}+3x-x+3>0 \\
 & x(-x+3)+1(-x+3)>0 \\
 & (x+1)(3-x)>0 \\
\end{align}\]
So, \[x>-1\] and \[x<3\] ………………….(5)
Here, the inequality equation that we have is \[{{\log }_{0.2}}\left( {{x}^{2}}-x-2 \right)>{{\log }_{0.2}}\left( -{{x}^{2}}+2x+3 \right)\] .
The base of the logarithm is 0.2 which is less than 1.
We know the property that inequality sign reverses while removing the log if the base of the logarithm is less than 1.
Now, using the property we can say that
\[{{\log }_{0.2}}\left( {{x}^{2}}-x-2 \right)>{{\log }_{0.2}}\left( -{{x}^{2}}+2x+3 \right)\]
\[\left( {{x}^{2}}-x-2 \right)<\left( -{{x}^{2}}+2x+3 \right)\] …………………..(6)
Solving equation (6), we get
\[\left( {{x}^{2}}-x-2 \right)<\left( -{{x}^{2}}+2x+3 \right)\]
\[\begin{align}
  & \left( {{x}^{2}}-x-2 \right)-\left( -{{x}^{2}}+2x+3 \right)<0 \\
 & {{x}^{2}}-x-2+{{x}^{2}}-2x-3<0 \\
 & 2{{x}^{2}}-3x-5<0 \\
\end{align}\]
Factorising the expression, we get
\[\begin{align}
  & 2{{x}^{2}}+2x-5x-5<0 \\
 & 2x(x+1)-5(x+1)<0 \\
 & (2x-5)(x+1)<0 \\
\end{align}\]
So, \[x<\dfrac{5}{2}\] and \[x>-1\] …………………….(7)
From equation (4), equation (5) and equation (7), we have the values of x.
We have to take the intersection of the values of x.

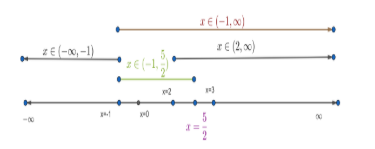
The intersection is common values of all the solutions that we have got
Here, the intersection is \[\left( 2,\dfrac{5}{2} \right)\] .

Note: In this question, one might do a mistake while removing the log terms from the equation \[{{\log }_{0.2}}\left( {{x}^{2}}-x-2 \right)>{{\log }_{0.2}}\left( -{{x}^{2}}+2x+3 \right)\] . After removing the log one may write it as \[\left( {{x}^{2}}-x-2 \right)>\left( -{{x}^{2}}+2x+3 \right)\] which as wrong. We have to keep the property in mind that inequality sign reverses while removing the log if the base of the logarithm is less than 1.