Question

Solve the following inequality graphically in two-dimensional plane:
$x - y \leqslant 2$

Answer 1

Hint: To solve any inequality graphically, first we have to graph the equality and then determine the region the given inequality satisfies. The solution of any inequality is the region towards which all the points lying satisfy the given inequality.

Complete step-by-step solution:
We are given the inequality $x - y \leqslant 2$, and we are required to draw it graphically in a two-dimensional plane.
To solve the inequality graphically, we need to first draw the equality in the two-dimensional plane.
That is, we have to draw $x - y = 2$ in the two-dimensional plane.
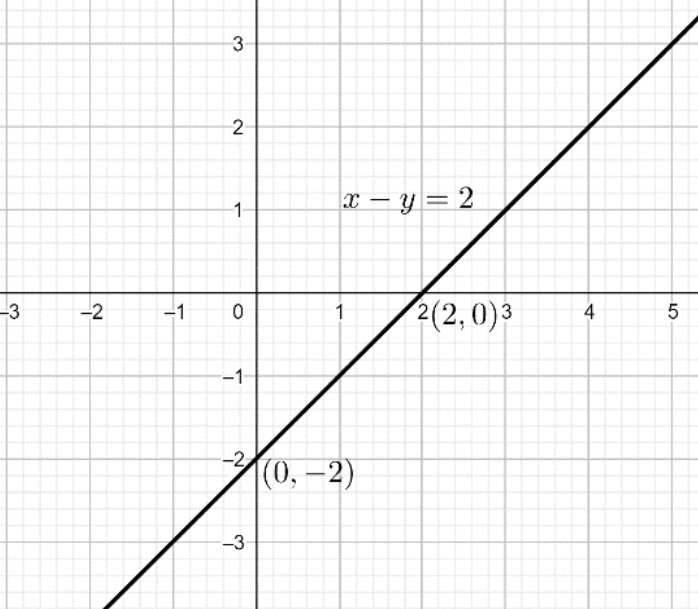
To draw this equality, we have to first determine the intercepts of the given equality.
First determine the $x$ intercept,
Substitute $y = 0$ in the given equality $x - y = 2$,
We get $x = 2$, so $x$ intercept is $2$.
Now, determine the $y$ intercept,
Substitute $x = 0$ in the given equality $x - y = 2$,
We get $y = - 2$, so $y$ intercept is $ - 2$.
Hence, we get the points $(2,0)$ and $(0, - 2)$.
To draw the graph of the equality $x - y = 2$, we will plot the above-mentioned points on the graph and then join the points.

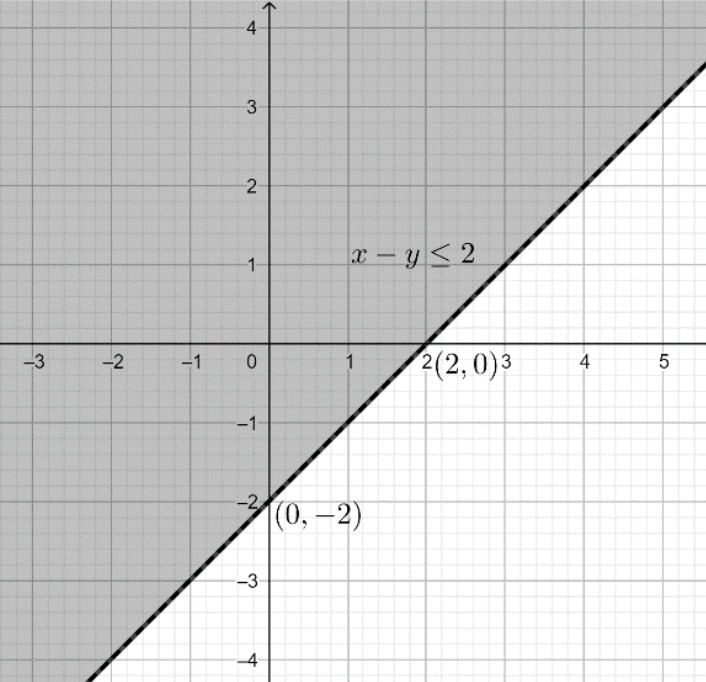
Now, we have to illustrate the inequality part, that is $x - y \leqslant 2$.
To check the solution of the inequality, we take any random point not lying on the graph of equality, say $(0,0)$, this point does not satisfy the equality $x - y = 2$.
Substitute the point $(0,0)$ in the inequality $x - y \leqslant 2$, and check if it satisfies the inequality or not.
Since $x - y = 0 - 0 = 0$ and $0 \leqslant 2$, so the point satisfies the inequality.
Hence, the solution of the inequality $x - y \leqslant 2$ is the region lying towards the selected point that is towards $(0,0)$. The shaded region in the below graph is the solution of the inequality $x - y \leqslant 2$.

Note: The points taken into consideration for determining the shaded region in the inequality should not lie on the graph of the equality, or it can be said that the points considered for determining the shaded region should not be the solution of the equality and not satisfy the equation.