
Solve the following inequality-
$\dfrac{{\left| {{\text{x}} + 2} \right| - {\text{x}}}}{{\text{x}}} < 2$
Answer
606k+ views
Hint: In this inequality, due to the presence of modulus sign, we will make two assumptions to eliminate the sign. In the two cases, one of them will be when the term is positive and the other for negative, that is-
$\left| {\text{k}} \right| = {\text{k}},\;{\text{k}} \geqslant 0$
$\left| {\text{k}} \right| = - {\text{k}},\;{\text{k < }}0$
Complete step-by-step answer:
We have been given the inequality-
$\dfrac{{\left| {{\text{x}} + 2} \right| - {\text{x}}}}{{\text{x}}} < 2$
$\begin{align}
&\dfrac{{\left| {{\text{x}} + 2} \right| - {\text{x}}}}{{\text{x}}} - 2 < 0 \\
&\dfrac{{\left| {{\text{x}} + 2} \right| - {\text{x}} - 2{\text{x}}}}{{\text{x}}} < 0 \\
&\dfrac{{\left| {{\text{x}} + 2} \right| - 3{\text{x}}}}{{\text{x}}} < 0 \\
\end{align} $
Now, we will eliminate the modulus sign, resulting in two cases-
$\begin{align}
&\left| {{\text{x}} + 2} \right| = {\text{x}} + 2,\;{\text{x}} + 2 \geqslant 0 \\
&\left| {{\text{x}} + 2} \right| = {\text{x}} + 2,\;{\text{x}} \geqslant - 2...\left( 1 \right) \\
&The\;second\;case\;is\;that - \\
&\left| {{\text{x}} + 2} \right| = - {\text{x}} - 2,\;{\text{x}} + 2 < 0 \\
&\left| {{\text{x}} + 2} \right| = - {\text{x}} - 2,\;{\text{x}} < - 2...\left( 2 \right) \\
\end{align} $
Substituting the value of $|x + 2|$ using equation (1)-
$\begin{align}
&\dfrac{{{\text{x}} + 2 - 3{\text{x}}}}{{\text{x}}} < 0 \\
&\dfrac{{2 - 2{\text{x}}}}{{\text{x}}} < 0 \\
&\dfrac{{2\left( {1 - {\text{x}}} \right)}}{{\text{x}}} < 0 \\
&The\;critical\;points\;are - \\
&{\text{x}} = 0\;and\;1 - {\text{x}} = 0 \\
&{\text{x}} = 0\;and\;{\text{x}} = 1 \\
\end{align} $
We will now represent the values of this function on the number line with respect to the critical points-
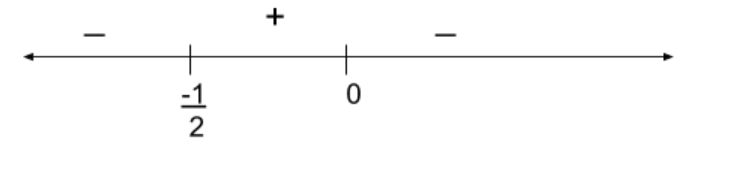
The sign above the three portions represent the value of the function at different values of x. As we can see, the function changes its sign at the critical values, that are 0 and 1. We can check this by substituting a suitable number in each of the three portions.
We need to find those values at which the function is negative. The function attains a negative value when x is less than zero or greater than 1. So, we can write that-
${\text{x}} \in \left( { - \infty ,0} \right) \cup \left( {1,\infty } \right)$
But while solving the modulus function, we assume that x is greater than or equal to -2 in equation (1). So, the correct range of values of x are-
$x \in \left[ { - 2,\;0} \right) \cup \left( {1,\infty } \right)...(3)$
Substituting the value of $|x + 2|$ using equation (2)-
$\begin{align}
&\dfrac{{ - {\text{x}} - 2 - 3{\text{x}}}}{{\text{x}}} < 0 \\
&\dfrac{{ - 2 - 4{\text{x}}}}{{\text{x}}} < 0 \\
&\dfrac{{2\left( { - 1 - 2{\text{x}}} \right)}}{{\text{x}}} < 0 \\
&The\;critical\;points\;are - \\
&{\text{x}} = 0\;and\; - 1 - 2{\text{x}} = 0 \\
&{\text{x}} = 0\;and\;{\text{x}} = - \dfrac{1}{2} \\
\end{align} $
We will now represent the values of this function on the number line with respect to the critical points-
The sign above the three portions represent the value of the function at different values of x. As we can see, the function changes its sign at the critical values, that are 0 and $-\dfrac{1}{2}$ We can check this by substituting a suitable number in each of the three portions.
We need to find those values at which the function is negative. The function attains a negative value when x is less than $-\dfrac{1}{2}$ or greater than 0. So, we can write that-
${\text{x}} \in \left( { - \infty , - \dfrac{1}{2}} \right) \cup \left( {0,\infty } \right)$
But while solving the modulus function, we assume that x is less than -2 in equation (2). So, the correct range of values of x are-
${\text{x}} \in \left( { - \infty , - 2} \right)...(4)$
Now, the range of values of x such that both the cases are inducted is when we take the union of equations (3) and (4), this can be done as-
${\text{x}} \in \left[ { - 2,\;0} \right) \cup \left( {1,\infty } \right) \cup \left( { - \infty , - 2} \right)$
${\text{x}} \in \left( { - \infty ,0} \right) \cup \left( {1.\infty } \right)$
These are the required range of values of x.
Note: In this question, a common mistake is that students directly cross multiply x in the inequality in the first step itself. This is completely wrong because we do not know the value of x, so when we cross multiply, if the value of x is negative, the sign should be reversed as well, but if we do not take both the cases, we are unknowingly eliminating one possibility that the value of x can be negative. So, we should always avoid cross multiplication of variables in questions related to inequalities.
$\left| {\text{k}} \right| = {\text{k}},\;{\text{k}} \geqslant 0$
$\left| {\text{k}} \right| = - {\text{k}},\;{\text{k < }}0$
Complete step-by-step answer:
We have been given the inequality-
$\dfrac{{\left| {{\text{x}} + 2} \right| - {\text{x}}}}{{\text{x}}} < 2$
$\begin{align}
&\dfrac{{\left| {{\text{x}} + 2} \right| - {\text{x}}}}{{\text{x}}} - 2 < 0 \\
&\dfrac{{\left| {{\text{x}} + 2} \right| - {\text{x}} - 2{\text{x}}}}{{\text{x}}} < 0 \\
&\dfrac{{\left| {{\text{x}} + 2} \right| - 3{\text{x}}}}{{\text{x}}} < 0 \\
\end{align} $
Now, we will eliminate the modulus sign, resulting in two cases-
$\begin{align}
&\left| {{\text{x}} + 2} \right| = {\text{x}} + 2,\;{\text{x}} + 2 \geqslant 0 \\
&\left| {{\text{x}} + 2} \right| = {\text{x}} + 2,\;{\text{x}} \geqslant - 2...\left( 1 \right) \\
&The\;second\;case\;is\;that - \\
&\left| {{\text{x}} + 2} \right| = - {\text{x}} - 2,\;{\text{x}} + 2 < 0 \\
&\left| {{\text{x}} + 2} \right| = - {\text{x}} - 2,\;{\text{x}} < - 2...\left( 2 \right) \\
\end{align} $
Substituting the value of $|x + 2|$ using equation (1)-
$\begin{align}
&\dfrac{{{\text{x}} + 2 - 3{\text{x}}}}{{\text{x}}} < 0 \\
&\dfrac{{2 - 2{\text{x}}}}{{\text{x}}} < 0 \\
&\dfrac{{2\left( {1 - {\text{x}}} \right)}}{{\text{x}}} < 0 \\
&The\;critical\;points\;are - \\
&{\text{x}} = 0\;and\;1 - {\text{x}} = 0 \\
&{\text{x}} = 0\;and\;{\text{x}} = 1 \\
\end{align} $
We will now represent the values of this function on the number line with respect to the critical points-
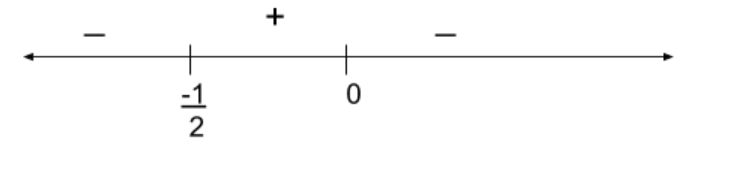
The sign above the three portions represent the value of the function at different values of x. As we can see, the function changes its sign at the critical values, that are 0 and 1. We can check this by substituting a suitable number in each of the three portions.
We need to find those values at which the function is negative. The function attains a negative value when x is less than zero or greater than 1. So, we can write that-
${\text{x}} \in \left( { - \infty ,0} \right) \cup \left( {1,\infty } \right)$
But while solving the modulus function, we assume that x is greater than or equal to -2 in equation (1). So, the correct range of values of x are-
$x \in \left[ { - 2,\;0} \right) \cup \left( {1,\infty } \right)...(3)$
Substituting the value of $|x + 2|$ using equation (2)-
$\begin{align}
&\dfrac{{ - {\text{x}} - 2 - 3{\text{x}}}}{{\text{x}}} < 0 \\
&\dfrac{{ - 2 - 4{\text{x}}}}{{\text{x}}} < 0 \\
&\dfrac{{2\left( { - 1 - 2{\text{x}}} \right)}}{{\text{x}}} < 0 \\
&The\;critical\;points\;are - \\
&{\text{x}} = 0\;and\; - 1 - 2{\text{x}} = 0 \\
&{\text{x}} = 0\;and\;{\text{x}} = - \dfrac{1}{2} \\
\end{align} $
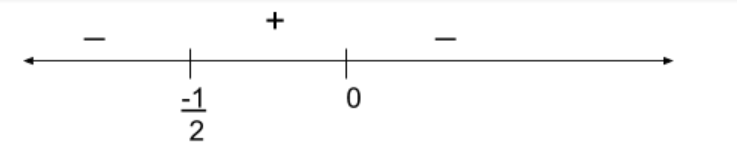
We will now represent the values of this function on the number line with respect to the critical points-

The sign above the three portions represent the value of the function at different values of x. As we can see, the function changes its sign at the critical values, that are 0 and $-\dfrac{1}{2}$ We can check this by substituting a suitable number in each of the three portions.
We need to find those values at which the function is negative. The function attains a negative value when x is less than $-\dfrac{1}{2}$ or greater than 0. So, we can write that-
${\text{x}} \in \left( { - \infty , - \dfrac{1}{2}} \right) \cup \left( {0,\infty } \right)$
But while solving the modulus function, we assume that x is less than -2 in equation (2). So, the correct range of values of x are-
${\text{x}} \in \left( { - \infty , - 2} \right)...(4)$
Now, the range of values of x such that both the cases are inducted is when we take the union of equations (3) and (4), this can be done as-
${\text{x}} \in \left[ { - 2,\;0} \right) \cup \left( {1,\infty } \right) \cup \left( { - \infty , - 2} \right)$
${\text{x}} \in \left( { - \infty ,0} \right) \cup \left( {1.\infty } \right)$
These are the required range of values of x.
Note: In this question, a common mistake is that students directly cross multiply x in the inequality in the first step itself. This is completely wrong because we do not know the value of x, so when we cross multiply, if the value of x is negative, the sign should be reversed as well, but if we do not take both the cases, we are unknowingly eliminating one possibility that the value of x can be negative. So, we should always avoid cross multiplication of variables in questions related to inequalities.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




