Question

Solve the following equations graphically.
\[3x - y = 7\] and \[2x + 3y = 1\] .

Answer 1

Hint: The following equations can be plotted on the graph taking value of one variable in terms of other variable , then we can put any integer in place of that variable to get a point on the graph and then another integer to obtain another point . Now join a straight line passing through those two points . Similarly , for the second equation obtain two points and then draw a line . Now , the point where these two lines intersect that point will provide the solution of these equations graphically .

Complete step-by-step solution:
Given : \[3x - y = 7\] and \[2x + 3y = 1\] .
Now , simplifying the first equation we get ,
\[y = 3x - 7\] .
Now putting \[x = 3\] we get ,
\[y = 3 \times 3 - 7\]
On solving we get ,
\[y = 2\]
Now putting \[x = 4\] we get ,
\[y = 3 \times 4 - 7\]
On solving we get ,
\[y = 5\]
Therefore we have points \[A\left( {3,2} \right)\] and \[B\left( {4,5} \right)\] . Now plotting them on graph we get ,

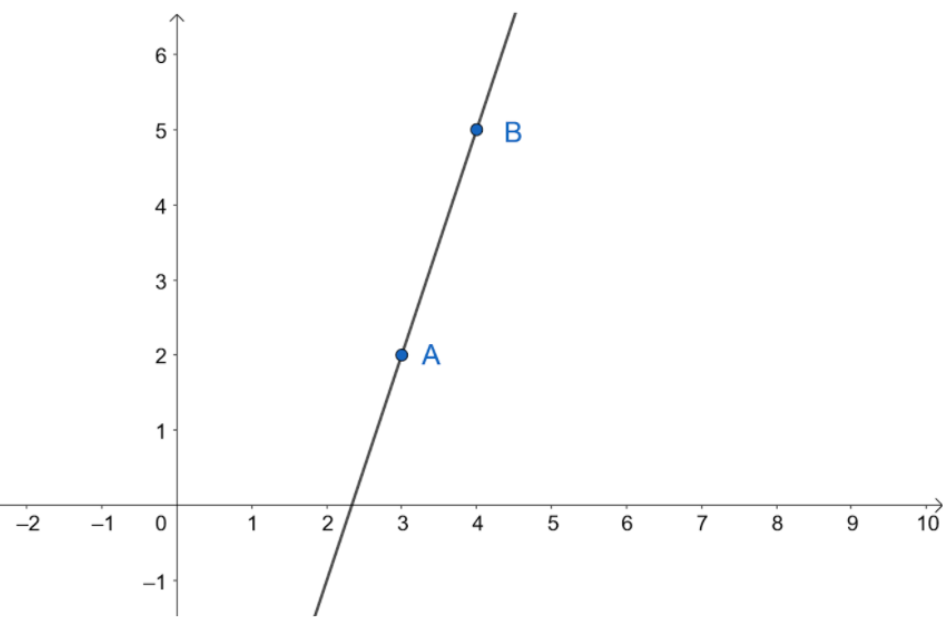
Now , simplifying the second equation we get ,
\[y = \dfrac{{1 - 2x}}{3}\]
Now putting \[x = 2\] we get ,
\[y = \dfrac{{1 - 2 \times 2}}{3}\]
On solving we get ,
\[y = - 1\] .
Now putting \[x = 5\] we get ,
\[y = \dfrac{{1 - 2 \times 5}}{3}\]
On solving we get ,
\[y = - 3\]
Therefore , we have points \[C\left( {2, - 1} \right)\] and \[C\left( {5, - 3} \right)\] . Now , plotting them on graph we get ,

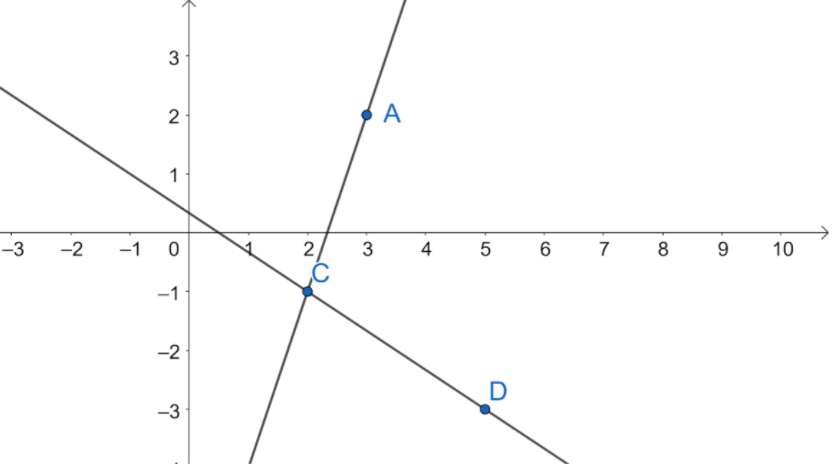
Now , from the second graph we can see that both the lines intersect at point \[C\left( {2, - 1} \right)\] . Therefore , it is the solution of the given equations .

Note: The solution of the given equations can also be obtained by using the substitution method , the value obtained from that can be used to verify the solution obtained from the graphical method . Always obtain two points for drawing a straight line to get accurate answers.