Question

How do you solve the equation $\left| 3x+6 \right|=9$ ?

Answer 1

Hint: We have given to solve a linear equation in one variable consisting of an absolute value function. We shall consider the absolute value function as a separate equation to be solved and the remaining constant term to be a separate function. Then, we will sketch the graphs of both the functions on the same plane and further obtain their points of intersection to compute our final solution.

Complete step by step solution:
Given that $\left| 3x+6 \right|=9$.
Let $f\left( x \right)=\left| 3x+6 \right|$ and let $g\left( x \right)=9$.
We shall sketch the graphs of both the functions taking each of them one-by-one.
In $f\left( x \right)=\left| 3x+6 \right|$, we can observe that this function resembles the absolute value function $\left| x \right|$ and can by modified as $f\left( x \right)=3\left| x+2 \right|$.
We know that the graph of $\left| x \right|$ is as follows:

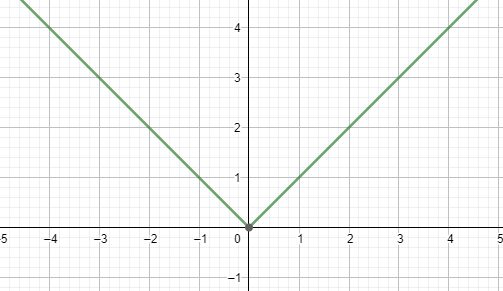
We will shift the graph 2 points towards the left of the x-axis first. Doing so, we will get the graph for $\left| x+3 \right|$ only. To change $f\left( x \right)$ to $\dfrac{f\left( x \right)}{3}$, we shall make the graph 3 points steeper, and thus the graph of $f\left( x \right)=3\left| x+2 \right|$ will look as follows:

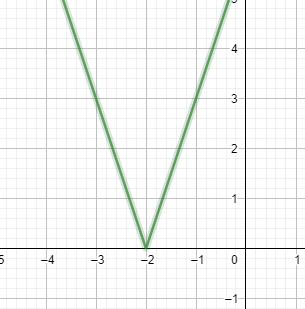
Now our second function$g\left( x \right)=9$, can also be written as $y=9$. In order to plot this constant function, we will draw a straight line parallel to the x-axis and passing through $y=0$ or the point $\left( 0,9 \right)$.
Thus, it is plotted as:

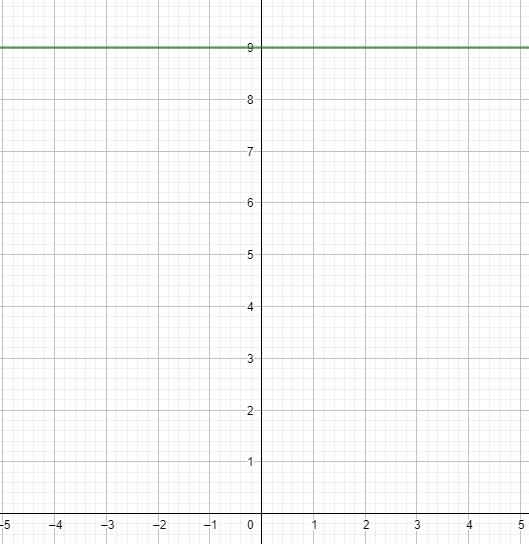
Finally, we shall sketch both the graphs shown above on the same plane.

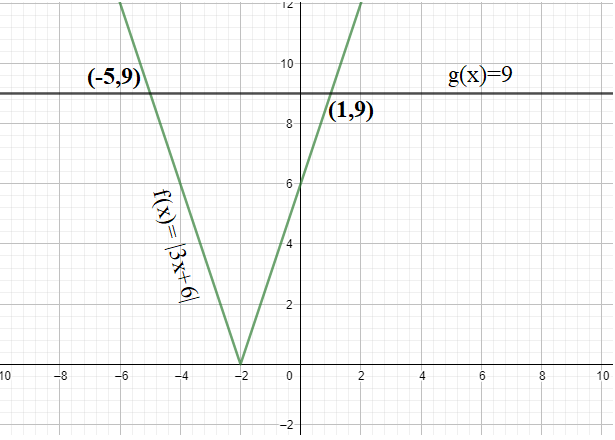
From this, we can observe that the graphs intersect at two points, $\left( 1,9 \right)$ and $\left( -5,9 \right)$.
Therefore, the solutions of the equation $\left| 3x+6 \right|=9$ are $x=1,-5$.

Note: Another method of finding the solutions was by the algebraic approach instead of the graphical one. We shall open the absolute modulus function with a positive and a negative sign one-by-one and then we shall solve the equations thus obtained to find the solutions for the given function.