
How do I solve $\sec x$ $\csc x$ = 2cscx in terms of [ 0, $2\pi $) ?
Answer
540k+ views
Hint: In this trigonometric problem, we have to solve the given equation and find the solution of ‘x’ in the range of [0,$2\pi $). We will be using reciprocal identities, trigonometric ratio tables for finding the value of angles. By following the values in quadrants, we will find the general solution in order to find ‘x’.
Complete step-by-step solution:
Now, let’s begin to solve the problem.
We will study some important terms and properties for solving this question. First let us see some reciprocal identities:
$\Rightarrow $cosec$\theta $ = $\dfrac{1}{\sin \theta }$ or sin$\theta $ = $\dfrac{1}{\cos ec\theta }$
$\Rightarrow $sec$\theta $ = $\dfrac{1}{\cos \theta }$ or cos$\theta $ = $\dfrac{1}{\sec \theta }$
$\Rightarrow $tan$\theta $ = $\dfrac{\sin \theta }{\cos \theta }$ = $\dfrac{1}{\cot \theta }$
$\Rightarrow $cot$\theta $ = $\dfrac{1}{\tan \theta }$ = $\dfrac{\cos \theta }{\sin \theta }$
For obtaining values at different angles, we have to go through the trigonometric ratio table:
Let’s study some properties of quadrants.
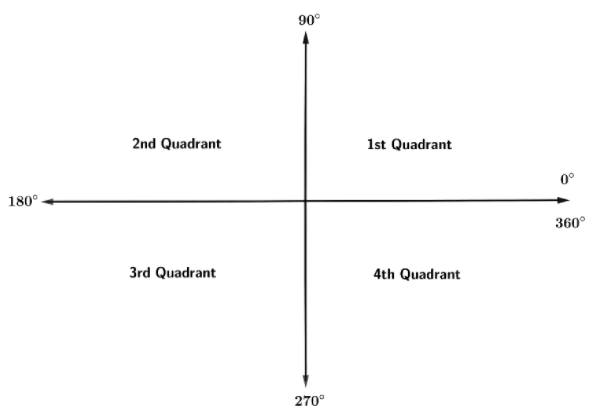
We can see from the above plane:
All angles of 1st quadrant lie in $0<\theta <90$ and the values of x and y both are positive.
For the 2nd quadrant, angles lie in $90<\theta <180$ where the values of x are negative and y are positive.
Similarly, in the 3rd quadrant, angles lie in $180<\theta <270$. The values of x and y both are negative.
And the 4th quadrant consists of the angles which lie in $270<\theta <360$. The values of x are positive whereas y are negative.
Let’s see the trigonometric values for sin and cos for different quadrants:
Now, write the given equation.
$\Rightarrow \sec x\cos ecx=2\cos ecx$
Move all the terms on the left hand side like this:
$\Rightarrow \sec x\cos ecx-2\cos ecx=0$
As we can see cosecx is common term, so take it outside:
$\Rightarrow \cos ecx\left( \sec x-2 \right)=0$
Take cosecx on the other side of the equation:
$\Rightarrow \sec x-2=0$
We can see from the table of trigonometric ratios we don’t have any such value as $\csc x$ =0 so we reject this.
From here, we can write:
$\Rightarrow \sec x=2......(i)$
As we know from reciprocal identities that :
secx = $\dfrac{1}{\cos x}......(ii)$
from equation(i) and equation(ii), we can write as:
$\Rightarrow \dfrac{1}{\cos x}=2$
On cross multiplying:
$\Rightarrow \cos x=\dfrac{1}{2}$
From trigonometric ratio table, we know that $\cos \dfrac{\pi }{3}=\dfrac{1}{2}$
As we know that cosine is positive in the first and fourth quadrants.
For general form of equations for cosx = cos$\theta $ :
$\Rightarrow x=2n\pi \pm \theta $
So,
$\Rightarrow x=2n\pi \pm \dfrac{\pi }{3}$
Solve for x now:
Put n = 0:
$\Rightarrow x=2(0)\pi +\dfrac{\pi }{3}\Leftrightarrow \dfrac{\pi }{3}$
Put n = 1:
$\Rightarrow x=2(1)\pi -\dfrac{\pi }{3}\Leftrightarrow \dfrac{5\pi }{3}$
So, it form solution within the range:
$\therefore x=\dfrac{\pi }{3},\dfrac{5\pi }{3}$
This is the final answer.
Note: We cannot leave the answer when we get $\cos x=\dfrac{1}{2}$ because we need to find the general solution as the range is being provided. Students should be aware of the basic properties of the trigonometric functions so that derived functions like secx and cosecx get easily solved.
Complete step-by-step solution:
Now, let’s begin to solve the problem.
We will study some important terms and properties for solving this question. First let us see some reciprocal identities:
$\Rightarrow $cosec$\theta $ = $\dfrac{1}{\sin \theta }$ or sin$\theta $ = $\dfrac{1}{\cos ec\theta }$
$\Rightarrow $sec$\theta $ = $\dfrac{1}{\cos \theta }$ or cos$\theta $ = $\dfrac{1}{\sec \theta }$
$\Rightarrow $tan$\theta $ = $\dfrac{\sin \theta }{\cos \theta }$ = $\dfrac{1}{\cot \theta }$
$\Rightarrow $cot$\theta $ = $\dfrac{1}{\tan \theta }$ = $\dfrac{\cos \theta }{\sin \theta }$
For obtaining values at different angles, we have to go through the trigonometric ratio table:
| Trigonometric ratios(angle $\theta $ in degrees) | ${{0}^{\circ }}$ | ${{30}^{\circ }}$ | ${{45}^{\circ }}$ | ${{60}^{\circ }}$ | ${{90}^{\circ }}$ |
| sin$\theta $ | 0 | $\dfrac{1}{2}$ | $\dfrac{1}{\sqrt{2}}$ | $\dfrac{\sqrt{3}}{2}$ | 1 |
| cos$\theta $ | 1 | $\dfrac{\sqrt{3}}{2}$ | $\dfrac{1}{\sqrt{2}}$ | $\dfrac{1}{2}$ | 0 |
| tan$\theta $ | 0 | $\dfrac{1}{\sqrt{3}}$ | 1 | $\sqrt{3}$ | $\infty $ |
| cosec$\theta $ | $\infty $ | 2 | $\sqrt{2}$ | $\dfrac{2}{\sqrt{3}}$ | 1 |
| sec$\theta $ | 1 | $\dfrac{2}{\sqrt{3}}$ | $\sqrt{2}$ | 2 | $\infty $ |
| cot$\theta $ | $\infty $ | $\sqrt{3}$ | 1 | $\dfrac{1}{\sqrt{3}}$ | 0 |
Let’s study some properties of quadrants.

We can see from the above plane:
All angles of 1st quadrant lie in $0<\theta <90$ and the values of x and y both are positive.
For the 2nd quadrant, angles lie in $90<\theta <180$ where the values of x are negative and y are positive.
Similarly, in the 3rd quadrant, angles lie in $180<\theta <270$. The values of x and y both are negative.
And the 4th quadrant consists of the angles which lie in $270<\theta <360$. The values of x are positive whereas y are negative.
Let’s see the trigonometric values for sin and cos for different quadrants:
| Trigonometric function | 1st quadrant | 2nd quadrant | 3rd quadrant | 4th quadrant |
| sin$\left( \theta \right)$ | +ve | +ve | -ve | -ve |
| cos$\left( \theta \right)$ | +ve | -ve | -ve | +ve |
Now, write the given equation.
$\Rightarrow \sec x\cos ecx=2\cos ecx$
Move all the terms on the left hand side like this:
$\Rightarrow \sec x\cos ecx-2\cos ecx=0$
As we can see cosecx is common term, so take it outside:
$\Rightarrow \cos ecx\left( \sec x-2 \right)=0$
Take cosecx on the other side of the equation:
$\Rightarrow \sec x-2=0$
We can see from the table of trigonometric ratios we don’t have any such value as $\csc x$ =0 so we reject this.
From here, we can write:
$\Rightarrow \sec x=2......(i)$
As we know from reciprocal identities that :
secx = $\dfrac{1}{\cos x}......(ii)$
from equation(i) and equation(ii), we can write as:
$\Rightarrow \dfrac{1}{\cos x}=2$
On cross multiplying:
$\Rightarrow \cos x=\dfrac{1}{2}$
From trigonometric ratio table, we know that $\cos \dfrac{\pi }{3}=\dfrac{1}{2}$
As we know that cosine is positive in the first and fourth quadrants.
For general form of equations for cosx = cos$\theta $ :
$\Rightarrow x=2n\pi \pm \theta $
So,
$\Rightarrow x=2n\pi \pm \dfrac{\pi }{3}$
Solve for x now:
Put n = 0:
$\Rightarrow x=2(0)\pi +\dfrac{\pi }{3}\Leftrightarrow \dfrac{\pi }{3}$
Put n = 1:
$\Rightarrow x=2(1)\pi -\dfrac{\pi }{3}\Leftrightarrow \dfrac{5\pi }{3}$
So, it form solution within the range:
$\therefore x=\dfrac{\pi }{3},\dfrac{5\pi }{3}$
This is the final answer.
Note: We cannot leave the answer when we get $\cos x=\dfrac{1}{2}$ because we need to find the general solution as the range is being provided. Students should be aware of the basic properties of the trigonometric functions so that derived functions like secx and cosecx get easily solved.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 8 Maths: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE




