
How do you solve $\dfrac{x}{{x - 3}} > 0$ using a sign chart?
Answer
515.1k+ views
Hint: In order to solve the given function consider the function as $\dfrac{{f\left( x \right)}}{{g\left( x \right)}}$, check whether any one of the function either $f\left( x \right)$or $g\left( x \right)$, changes its sign or not. Then square the denominator to make it positive then marks the values at which the function sign will change on the number line. Mark them as positive or negative parts.
Complete step by step solution:
We are given with the function $\dfrac{x}{{x - 3}} > 0$, let’s consider this as $\dfrac{{f\left( x \right)}}{{g\left( x \right)}}$.
Checking for $f\left( x \right)$, that at which part its sign changes and we get:
$f\left( x \right) = x$ and its sign will only change at $x = 0$.
Next look for the second function $g\left( x \right)$ and we get:
$f\left( x \right) = x - 3$ and its sign will only change at $x = 3$.
In the function $\dfrac{x}{{x - 3}} > 0$, we can see that when we put $x = 3$, the denominator becomes zero, which will give indeterminate value, and if we $x < 3$ for the denominator it will give negative value. So, make the denominator positive by Multiplying and dividing the denominator by $x - 3$, and we get:
$\dfrac{{x\left( {x - 3} \right)}}{{{{\left( {x - 3} \right)}^2}}} > 0 = > x\left( {x - 3} \right) > 0$
We have two points to mark at the number $x = 0$ and $x = 3$. Mark them and write their signs accordingly and we get:
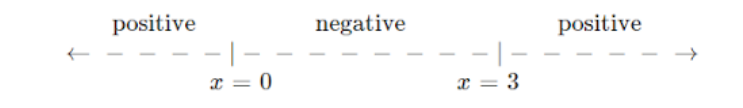
Since, we know that the left side of the point is always positive and in $x\left( {x - 3} \right) > 0$, $x - 3$ has the power $1$ which is odd so the sign will change to negative on the left side of $x = 3$, similarly for x has also the power $1$ which is odd so again the sign will change to positive.
And this is how the sign chart works for the functions
Note: I.Different functions will have different denominators, first find their value by comparing it to zero.
II.Always Square the denominator to make it positive.
III.Remove the indeterminate form, by avoiding the value that gives this form.
Complete step by step solution:
We are given with the function $\dfrac{x}{{x - 3}} > 0$, let’s consider this as $\dfrac{{f\left( x \right)}}{{g\left( x \right)}}$.
Checking for $f\left( x \right)$, that at which part its sign changes and we get:
$f\left( x \right) = x$ and its sign will only change at $x = 0$.
Next look for the second function $g\left( x \right)$ and we get:
$f\left( x \right) = x - 3$ and its sign will only change at $x = 3$.
In the function $\dfrac{x}{{x - 3}} > 0$, we can see that when we put $x = 3$, the denominator becomes zero, which will give indeterminate value, and if we $x < 3$ for the denominator it will give negative value. So, make the denominator positive by Multiplying and dividing the denominator by $x - 3$, and we get:
$\dfrac{{x\left( {x - 3} \right)}}{{{{\left( {x - 3} \right)}^2}}} > 0 = > x\left( {x - 3} \right) > 0$
We have two points to mark at the number $x = 0$ and $x = 3$. Mark them and write their signs accordingly and we get:
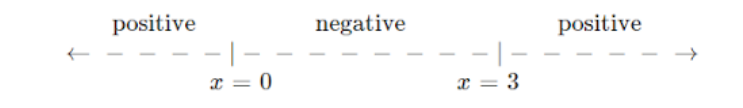
Since, we know that the left side of the point is always positive and in $x\left( {x - 3} \right) > 0$, $x - 3$ has the power $1$ which is odd so the sign will change to negative on the left side of $x = 3$, similarly for x has also the power $1$ which is odd so again the sign will change to positive.
And this is how the sign chart works for the functions
Note: I.Different functions will have different denominators, first find their value by comparing it to zero.
II.Always Square the denominator to make it positive.
III.Remove the indeterminate form, by avoiding the value that gives this form.
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Which of the following does not have a fundamental class 10 physics CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




