Question

How do you solve $\dfrac{1}{3}{{x}^{2}}-3=0$ by graphing?

Answer 1

Hint: We can find the roots of the equation $y=f\left( x \right)$ by drawing the graph of $f\left( x \right)$ in the Cartesian plane and check where the graph will cut x axis. If the graph never cuts the x axis then there will be no possible real root for the equation $y=f\left( x \right)$. The graph of the quadratic equation is a parabola. It may be an upward or downward parabola depending on the leading coefficient. If the leading coefficient is greater than 0 then it is an upward parabola otherwise it is a downward parabola.

Complete step by step answer:
The given equation is $\dfrac{1}{3}{{x}^{2}}-3=0$ by solving further, we get ${{x}^{2}}-9=0$ .
One method is by solving it graphically is drawing the graph ${{x}^{2}}-9=0$ and check the x intercept and another method is drawing the graph $y={{x}^{2}}$ and $y=9$ check the intersecting point of the 2 graphs .
Let’s try the second method. So drawing $y={{x}^{2}}$ and $y=9$ .

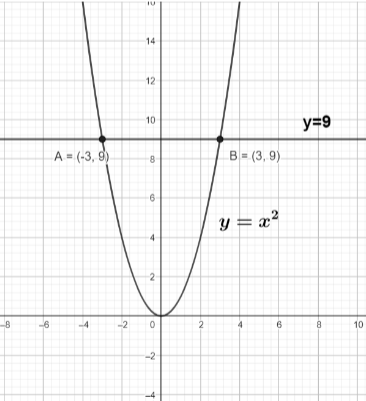
We can clearly see two curve one is $y={{x}^{2}}$ and another is $y=9$ and we can see the intersecting point A and B where $A=\left( -3,9 \right)$ and $B=\left( 3,9 \right)$ so the solution to the equation $\dfrac{1}{3}{{x}^{2}}-3=0$ is -3 or 3.
Let’s try the first method which involves directly drawing the graph $y={{x}^{2}}-9$ and checking the x intercept.

The graph $y={{x}^{2}}-9$ is 9 units down of the graph $y={{x}^{2}}$ .

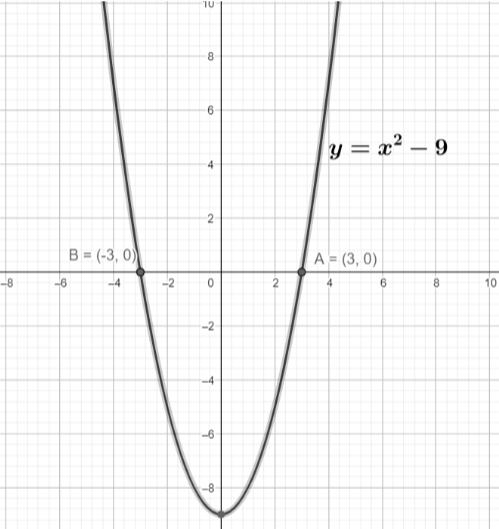
Now we can check the x intercept is -3 and 3. So the roots of the equation are -3 and 3.

Note: When solving graphically sometimes we can’t draw the graph of a function. In that case do apply the second method that we have used earlier in the above question. For example if you have a question like this “How many real roots of are possible for the equation $x-\tan x=0$ in between 0 to $2\pi $ “ .it is very difficult to draw the graph $x-\tan x$ so first draw the graph $y=x$ and then $y=\tan x$ check the number of intersecting point between 0 and $2\pi $ .