Question

How do you solve by substitution $y=3x-4$ and $9x-3y=14$?

Answer 1

Hint: There are two unknowns $x$ and $y$ and also two equations to solve. First, we are applying the process of substitution and then reduction. We take the value of one variable from one equation and put it into the other one. We solve the equations equating the coefficients of one variable and omitting the variable. The other variable remains with the constants. Using the binary operation, we find the value of the other variable.

Complete step-by-step solution:
The given equations $y=3x-4$ and $9x-3y=14$ are linear equations of two variables.
We know that the number of equations has to be equal to the number of unknowns to solve them. We take the equations as $y=3x-4.....(i)$ and $9x-3y=14......(ii)$.
We find the value of one variable $y$ with respect to $x$ based on the equation $y=3x-4$. We replace the value of $y$ in the second equation of $9x-3y=14$ and get
\[\begin{align}
  & 9x-3y=14 \\
 & \Rightarrow 9x-3\left( 3x-4 \right)=14 \\
 & \Rightarrow 9x-9x+12=14 \\
 & \Rightarrow 12=14 \\
\end{align}\]
There remains no variable to solve the equations.
The equations $y=3x-4$ and $9x-3y=14$ have no solutions.

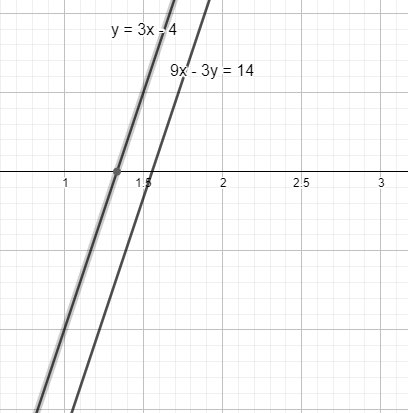
The lines are parallel to each other.

Note: We can also find the conditions for the number of solutions of two equations
$ax+by=m$ and $cx+dy=n$.
If $\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{m}{n}$ then the equations have an infinite number of solutions.
If $\dfrac{a}{c}\ne \dfrac{b}{d}$ then the equations have only one solution.
If $\dfrac{a}{c}=\dfrac{b}{d}\ne \dfrac{m}{n}$ then the equations have no solution.
For our equations $y=3x-4$ and $9x-3y=14$, we have $3x-y=4$ and $9x-3y=14$.
The ratios are $\dfrac{3}{9},\dfrac{-1}{-3},\dfrac{4}{14}$. The relation is $\dfrac{3}{9}=\dfrac{-1}{-3}\ne \dfrac{4}{14}$.
Therefore, there are no solutions for $y=3x-4$ and $9x-3y=14$.