Question

How do you solve and graph the absolute value inequality $\left| 2x+4 \right|>8$?

Answer 1

Hint: To solve the inequality given in the above problem is as follows: $\left| 2x+4 \right|>8$. We know that if we have to solve the modulus inequality of this form $\left| x+a \right|>b$ then we will convert this modulus form as follows: $\left( x+a \right)<-b$ and taking union with $\left( x+a \right)>b$. This result of union gives us the solution of the above inequality. And using this solution, we can draw the graph also.

Complete step-by-step solution:
The inequality of modulus form given in the above problem is as follows:
$\left| 2x+4 \right|>8$
Now, we are going to solve the above inequality by opening this modulus form and we get,
$\begin{align}
  & \Rightarrow \left( 2x+4 \right)<-8, \\
 & \Rightarrow \left( 2x+4 \right)>8 \\
\end{align}$
Solving the above two inequalities one by one and then taking union of these two inequality solutions.
Solving the first inequality in the above we get,
$\Rightarrow 2x+4<-8$
Subtracting 4 on both the sides in the above expression we get,
$\begin{align}
  & \Rightarrow 2x+4-4<-8-4 \\
 & \Rightarrow 2x<-12 \\
\end{align}$
Dividing 2 on both the sides we get,
$\begin{align}
  & \Rightarrow \dfrac{2x}{2}<-\dfrac{12}{2} \\
 & \Rightarrow x<-6 \\
\end{align}$
Solving the second inequality we get,
$\Rightarrow 2x+4>8$
Subtracting 4 on both the sides we get,
$\begin{align}
  & \Rightarrow 2x+4-4>8-4 \\
 & \Rightarrow 2x>4 \\
\end{align}$
Dividing 2 on both the sides we get,
$\begin{align}
  & \Rightarrow \dfrac{2x}{2}>\dfrac{4}{2} \\
 & \Rightarrow x>2 \\
\end{align}$
Now, taking union of the solution of the above two inequalities we get,
$\left( x<-6 \right)\bigcup \left( x>2 \right)$
Now, converting the above inequalities into interval notation we get,
Converting $\left( x<-6 \right)$ into interval notation we get,
$\Rightarrow x\in \left( -\infty ,-6 \right)$
Converting $\left( x>2 \right)$ into interval notation we get,
$\Rightarrow x\in \left( 2,\infty \right)$
Now, union of the above two intervals are as follows:
$x\in \left( -\infty ,-6 \right)\bigcup \left( 2,\infty \right)$
Hence, the solution of the inequality given above is as follows:
$x\in \left( -\infty ,-6 \right)\bigcup \left( 2,\infty \right)$
Now, we are going to draw the graph of the above inequality. For that, first of all, we are going to draw the graph of the modulus function.
The function written in the modulus is as follows:
$\left| 2x+4 \right|$
The graph of this function is as follows:

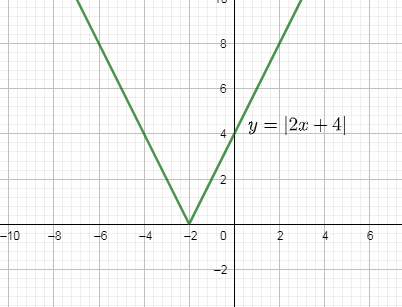
Now, in the above problem we need the values when y takes value greater than 8 so we will eliminate the area in the above graph where y’s value is less than or equal to 8.

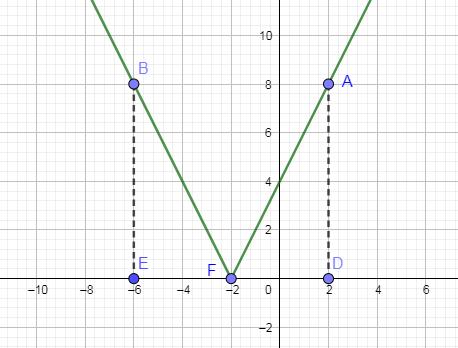
In the above graph, as you can see that when the value of function is 8 then two x values are coming i.e. (2 and -6) so we are removing the portion BFA from the above graph to get the required graph.

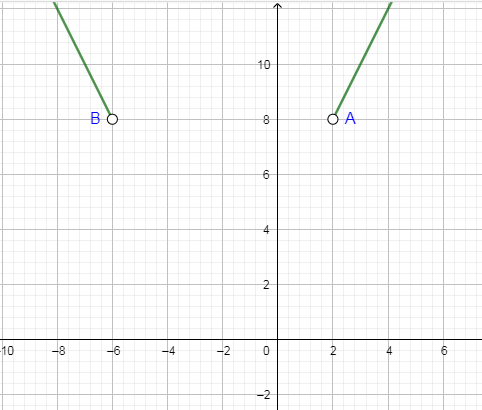
The open holes of points A and B are suggesting that at x equals -6 and 2 the y is not taking a value. Hence, we have drawn the graph of $\left| 2x+4 \right|>8$.

Note: As you can see that the graph we have drawn above lies in the same interval in which we have calculated the solution for the inequality. The solution of the inequality $\left| 2x+4 \right|>8$ is as follows:
$x\in \left( -\infty ,-6 \right)\bigcup \left( 2,\infty \right)$
And the graph which we have drawn above is as follows:

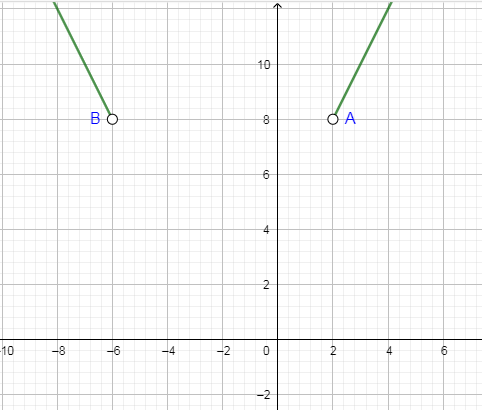
Now, you can see that in the above graph the value of x lies from negative infinity to -6( in which -6 is not included) and from 2 to infinity (in which 2 is not included).
So, basically, graphical representation is a proof that the solution which we have found is correct.