Question

How do you solve and graph for $\dfrac{x}{4} < 9?$

Answer 1

Hint:First of all, solve the given inequality for the value of $x$ then replace the inequality with equality sign and then draw the graph for the equation. Now pick up any point other than on the graph of the equation and check it on the inequality, if it satisfies it then shade portion of the point’s side and if not then shade the opposite side. Also if inequality does not contain an equality sign, then draw a dotted line.

Complete step by step solution:
To solve and graph the given inequality $\dfrac{x}{4} < 9$, we will first
solve it for the value of $x$ as follows
$ \Rightarrow \dfrac{x}{4} < 9$
Multiplying both sides with $4$
$
\Rightarrow 4 \times \dfrac{x}{4} < 4 \times 9 \\
\Rightarrow x < 36 \\
$
We get the required solution, expressing it in interval form, we will get
$x \in ( - \infty ,\;36)$
Now, writing the inequality after as normal equation in order to plot its graph
$ \Rightarrow x = 36$
If we plot it in a Cartesian plane, we know that $x = a$ gives a line parallel to y-axis passing from point $(a,\;0)$
So graph of $x = 36$ will be drawn as follows

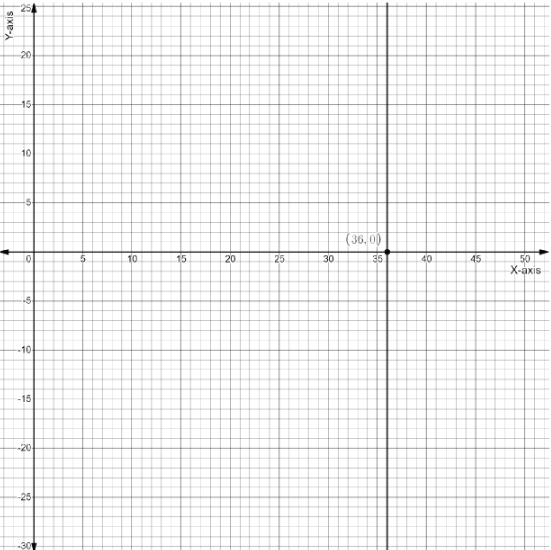
Now, coming to inequality $x < 36$
Checking it for point $(0,\;0)$
$ \Rightarrow 0 < 36$
$(0,\;0)$ holds true for the inequality, therefore we will shade its side and also the inequality do not includes $36$ so we will draw dotted line

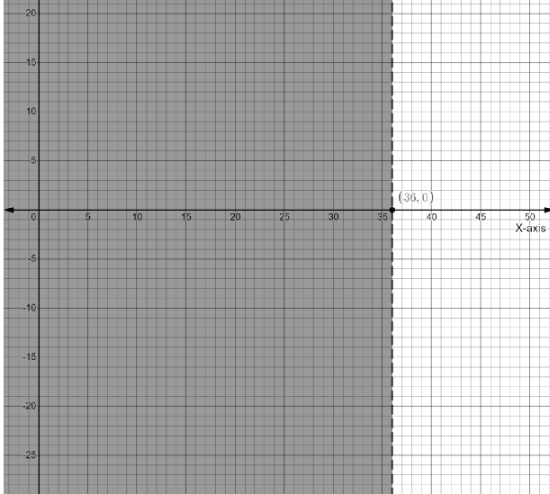
This is the required graph for the given inequality.

Note: When checking for any point, try to check for the origin (given that it does not exist on the graph of the equation), origin is the simplest point you can check for, just put zero in the equation and check if it satisfies the inequality or not.