Question

How do you solve and check your solution to \[c - \dfrac{3}{5} = \dfrac{5}{6}\]?

Answer 1

Hint:Here in this we have to solve the given equation and it is in the form of an algebraic equation. Solving this equation, we have to find the unknown value c. The LHS and RHS of the given equation is in the form of fraction. by using the simple multiplication and division we find the value of c.

Complete step by step explanation:
The given equation is an algebraic equation. The algebraic equation is a combination of variable and constant which has an equal sign. Here the equation is in the form of fraction in LHS and RHS. So we use multiplication and division or arithmetic operations and solve for further Now consider the given equation
\[c - \dfrac{3}{5} = \dfrac{5}{6}\]
Add \[\dfrac{3}{5}\] on both sides to the above equation
\[ \Rightarrow c - \dfrac{3}{5} + \dfrac{3}{5} = \dfrac{5}{6} + \dfrac{3}{5}\]
On simplifying we get
\[ \Rightarrow c = \dfrac{5}{6} + \dfrac{3}{5}\]
Since we are adding the two fractions, let we take LCM for the numbers 6 and 5

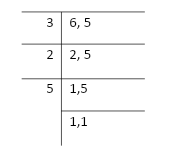
Therefore the LCM of 6 and 5 is \[3 \times 2 \times 5 = 30\]
\[ \Rightarrow c = \dfrac{{\dfrac{5}{6} \times 30 + \dfrac{3}{5} \times 30}}{{30}}\]
On simplifying we have
\[ \Rightarrow c = \dfrac{{5 \times 5 + 3 \times 6}}{{30}}\]
\[ \Rightarrow c = \dfrac{{25 + 18}}{{30}}\]
On further simplification
\[ \Rightarrow c = \dfrac{{43}}{{30}}\]
The numerator is a prime number. There will be no common for the both numerator and
denominator. Therefore, the value of c is \[\dfrac{{43}}{{30}}\]
We can also verify the given question by substituting the value of c.
Consider\[c - \dfrac{3}{5} = \dfrac{5}{6}\] Substitute the value of c as \[\dfrac{{43}}{{30}}\] so we have \[ \Rightarrow \dfrac{{43}}{{30}} - \dfrac{3}{5} = \dfrac{5}{6}\]
Since we are subtracting the two fractions, let we take LCM for the numbers 30 and 5

Since we are sub Therefore the LCM of 30 and 5 is \[3 \times 2 \times 5 = 30\]
\[ \Rightarrow \dfrac{{\dfrac{{43}}{{30}} \times 30 - \dfrac{3}{5} \times 30}}{{30}} = \dfrac{5}{6}\]
On simplifying we have
\[ \Rightarrow \dfrac{{43 - 3 \times 6}}{{30}} = \dfrac{5}{6}\]
\[ \Rightarrow \dfrac{{43 - 18}}{{30}} = \dfrac{5}{6}\]
On further simplification
\[ \Rightarrow \dfrac{{25}}{{30}} = \dfrac{5}{6}\]
Divide the both numerator and denominator by 5 we have
\[ \Rightarrow \dfrac{5}{6} = \dfrac{5}{6}\]
Hence LHS is equal to RHS.

Note: If the algebraic expression contains only one unknown, we determine the value by using simple multiplication and division. The function contains a fraction then there is no change in solving the algebraic expression. The tables of multiplication should be known to solve these kinds of problems. tracking the two fractions, let we take LCM for the numbers 30 and 5