Question

How do you solve \[2\log x=\log 2+\log \left( 3x-4 \right)\]?

Answer 1

Hint: Use the formula \[a\log m=\log {{m}^{a}}\] to simplify the term in L.H.S. Now, consider the expression in the R.H.S. and use the sum to product rule of logarithm given as: - \[\log m+\log n=\log \left( mn \right)\], to simplify the R.H.S. Remove the log function from both the sides and form a quadratic equation in x. Solve this quadratic equation using the middle term split method and find the two values of x. Reject the invalid value of x, if present, by using the information that ‘argument of the logarithmic function must be greater than 0’.

Complete step by step solution:
Here, we have been provided with the logarithmic equation: \[2\log x=\log 2+\log \left( 3x-4 \right)\] and we are asked to solve it. That means we need to find the values of x.
Now, using the identity: - \[a\log m=\log {{m}^{a}}\] in the L.H.S. of the given expression, we get,
\[\Rightarrow \log \left( {{x}^{2}} \right)=\log 2+\log \left( 3x-4 \right)\]
Using the sum to product rule of log given as: - \[\log m+\log n=\log \left( mn \right)\] in the R.H.S., we get,
\[\begin{align}
  & \Rightarrow \log \left( {{x}^{2}} \right)=\log \left( 2\times \left( 3x-4 \right) \right) \\
 & \Rightarrow \log \left( {{x}^{2}} \right)=\log \left( 6x-8 \right) \\
\end{align}\]
As we can see that we have not been provided with the base of the logarithm, so we will assume that it is a common log expression, that means log to the base 10. So, we have,
\[\Rightarrow {{\log }_{10}}\left( {{x}^{2}} \right)={{\log }_{10}}\left( 6x-8 \right)\]
Clearly, we can see that we have log with the same base on both sides, so we can remove the log function and equate their argument. So, we get,
\[\begin{align}
  & \Rightarrow {{x}^{2}}=6x-8 \\
 & \Rightarrow {{x}^{2}}-6x+8=0 \\
\end{align}\]
Clearly, we can see that the above equation is a quadratic equation in x, so using the middle term split method, we have,
\[\begin{align}
  & \Rightarrow {{x}^{2}}-4x-2x+8=0 \\
 & \Rightarrow x\left( x-4 \right)-2\left( x-4 \right)=0 \\
 & \Rightarrow \left( x-4 \right)\left( x-2 \right)=0 \\
\end{align}\]
Substituting each term equal to 0, we get,
\[\Rightarrow x=4\] or x = 2
Here, we have obtained two solutions, let us check if both the values of x are valid or not. Since, we know that for a log function to be defined we must have its argument greater than 0, so from the given logarithmic equation we must have,
(i) \[x>0\Rightarrow x\in \left( 0,\infty \right)\]
(ii) \[3x-4>0\Rightarrow x>\dfrac{4}{3}\Rightarrow x\in \left( \dfrac{4}{3},\infty \right)\]
Since, we need to satisfy both the conditions (i) and (ii), so we need to consider the intersection of the two sets of values of x. Therefore, we have,

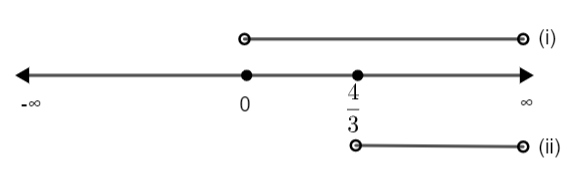
So, we can say that \[x\in \left( \dfrac{4}{3},\infty \right)\] is the final condition. Clearly, we can see that both the obtained values of x, i.e., 2 and 4, satisfy the conditions obtained.
Hence, the solutions of the given logarithmic equation are: - x = 2 or x = 4.

Note: One may make a mistake by thinking that the L.H.S. expression \[2\log x\] is already defined since we have used the conversion \[2\log x=\log \left( {{x}^{2}} \right)\]. But this is not true, actually we have to consider the initial equation and not its simplified form and that is the reason we have considered inequality (i). Remember some basic formulas of logarithm given as: - \[\log m+\log n=\log \left( mn \right)\], \[\log m-\log n=\log \left( \dfrac{m}{n} \right)\], \[\log {{m}^{a}}=a\log m\] etc. Always check if the obtained values of x are valid or not.