Question

How do you solve \[18 - 3x < 12\] and graph the solution on a number line?

Answer 1

Hint:For any inequality when you are solving you should know the sign of inequality changes when you multiply minus sign both the side, and rest solution can be done same as that for equals sign is done, nor any other assumption should be needed.

Complete step by step solution:
For the given question \[18 - 3x < 12\]

Rearranging the terms we get:
\[
\Rightarrow - 3x < 12 - 18 \\
\Rightarrow - 3x < - 6 \\
\Rightarrow 3x >
6({\text{multiplying}}\,{\text{minus}}\,{\text{sign}}\,{\text{on}}\,{\text{both}}\,{\text{side}}\,{\text{
of}}\,{\text{bracket)}} \\
\Rightarrow {\text{x > 2}} \\
\]
Here we get the range of \[x\]that is it is greater than\[{\text{2}}\], which implies that the given quantity can have any possible value above \[{\text{2}}\]

Range of \[x\]can be written as\[(2,\infty )\], here open bracket “\[()\]” is indicating that the value written in the bracket is not for the quantity \[x\]but the very next closed value after\[{\text{2}}\] is the value of \[x\], and since infinity is not known so we always provide open bracket for infinity.

Graph:
 Here we have draw the graph on number line to show all the possible values of “x”

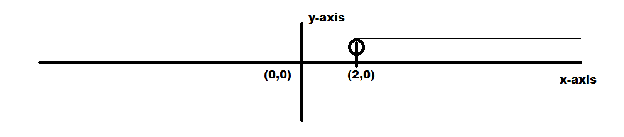
Additional Information: If you are given the equals to sign with inequalities then also the process would be same the only change would be in describing the range of the quantity, that is closed bracket would be used instead of open bracket.

Note: Inequality basically defines the region of the quantity whosoever for which the inequality is used for, that is it gives you a range of possible values for the quantity you are finding for. In this range real as well as complex range also occurs.