Question

Solid cylinder of diameter $12$ cm and height $15$ cm is melted and recast into toys with the shape of a right circular cone mounted on a hemisphere of radius $3$ cm. If the height of the toy is $12$ cm. Find the number of toys so formed.

Answer 1

Hint: To solve this question we need to have a knowledge of 3- D figures. The cylinder is melted and recast into a toy, which means the volume of material remains the same. The volume of cylinder is $\pi {{r}^{2}}h$, volume of toy is sum of volume of right circular cone and volume of hemisphere whose volume are $\dfrac{\pi }{3}{{r}^{2}}h$ and $\dfrac{2\pi }{3}{{r}^{3}}$respectively.

Complete step-by-step solution:
The question ask us to find the number of toys when a solid cylinder of $12$cm diameter and height of $15$ cm is melted and recast into a right circular cone mounted on a hemisphere where the radius of the hemisphere is $3$ cm and the height of the toy is $12$ cm. Below is the figure of the two shapes.

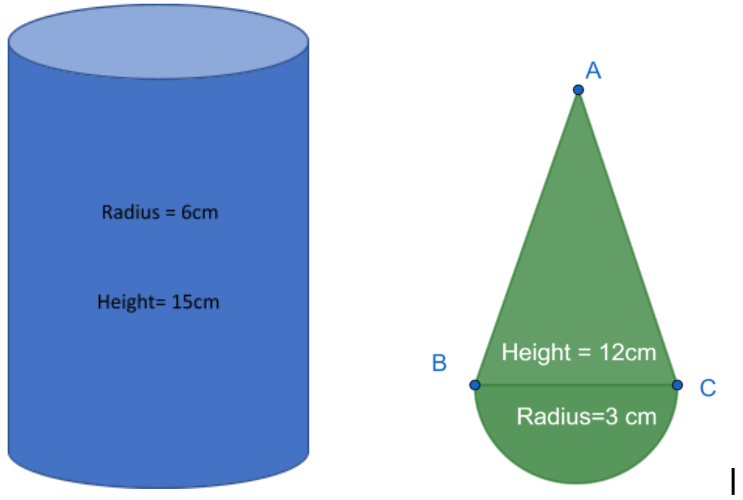
Now since the solid cylinder is melted and recast into a right circular cone mounted on a hemisphere to make a “n” toy so the volume of the material used will be the same as the whole amount of material is melted and recast into another object. So we will equate the volume of the cylinder with the volume of the “n” toys.
Volume of a toy is equal to the volume of right circular cone + volume of hemisphere, mathematically written as
$\text{Volume of a toy = Volume of cone + Volume of hemisphere}$
Since the volume is equated so the equation will be:
$\text{Volume of cylinder = n}\left( \text{Volume of a toy } \right)$
$\Rightarrow \text{Volume of cylinder = n}\left( \text{Volume of cone + Volume of hemisphere} \right)$
The volume of the cylinder is $\pi {{r}^{2}}h$. Volume of the cone is $\dfrac{1}{3}\pi {{r}^{2}}h$ . Volume of the hemisphere is $\dfrac{2\pi }{3}{{r}^{3}}$ . Here “r” is the radius and “h” is the height of the figure given.
$\Rightarrow \pi {{r}_{1}}^{2}{{h}_{1}}=n\left( \dfrac{\pi }{3}{{r}_{2}}^{2}{{h}_{2}}+\dfrac{2\pi }{3}r_{3}^{3} \right)$
In this case the radius of hemisphere and right circular cone is equal which is $3$cm. Radius of base of cylinder and height is $6$ cm and $15$ cm. Height of the cone is $9$ cm. On putting these values we get:
$\Rightarrow \pi \times {{6}^{2}}\times 15=n\left( \dfrac{\pi }{3}\times {{3}^{2}}\times 9+\dfrac{2\pi }{3}\times {{3}^{3}} \right)$
$\Rightarrow \pi \times 36\times 15=n\left( \dfrac{\pi }{3}\times 9\times 9+\dfrac{2\pi }{3}\times 27 \right)$
$\Rightarrow \pi \times 36\times 15=n\left( \dfrac{\pi }{3}\left( 9\times 9+2\times 27 \right) \right)$
$\Rightarrow \pi \times 36\times 15=n\left( \dfrac{\pi }{3}\left( 81+54 \right) \right)$
$\Rightarrow \pi \times 36\times 15=n\left( \dfrac{\pi }{3}\times 135 \right)$
On taking $\left( \dfrac{\pi }{3}\times 135 \right)$to R.H.S. The value on L.H.S. is divided by the term $\left( \dfrac{\pi }{3}\times 135 \right)$. On doing this we get:
$\Rightarrow n=\dfrac{\pi \times 36\times 15}{\left( \dfrac{\pi }{3}\times 135 \right)}$
$\Rightarrow n=\dfrac{\pi \times 36\times 15\times 3}{\pi \times 135}$
On dividing the numerator from denominator we get:
$\Rightarrow n=12$
$\therefore $ Total number of $12$ toys could be formed.

Note: To solve these types of questions we need to know the formula for the 3-Dimensional figures. Radius is half of the diameter for any figure. When a substance is melted and recast the volume is always conserved.