Question

What is the slope and intercept of \[3x + y = 5\]?

Answer 1

Hint: Let \[m\] be the slope of a line and \[c\] its intercept on y-axis. Then the equation of this straight line is written as \[y = mx + c\] and this form is known as slope intercept form. So by comparing the given expression with slope intercept form we can easily find the slope and intercept.
Formula used:
 Slope intercept form (standard form of equation of a straight line)
\[y = mx + c\]; In which m is the slope of line and $c$ is the intercept on y-axis

Complete step-by-step solution:
Step 1: Conversion of given expression (\[3x + y = 5\]) into slope intercept form
We know that slope intercept form is given by
 \[y = mx + c\]...........................Equation-1
Where m is the slope and c is the intercept on y-axis
Now by rearranging terms we get
\[3x + y = 5\]
\[ - y = 3x - 5\]
Step 2: Multiplying left hand side and right hand side with \[ - 1\], we get
\[ - y = 3x - 5\]
\[( - 1) \times ( - y) = ( - 1) \times (3x - 5)\]
Multiplying \[( - 1)\] with \[( - y)\], we get
\[y = ( - 1) \times (3x - 5)\]
Multiplying \[( - 1)\]with\[(3x - 5)\], we get
\[y = - 3x + 5\]..............................Equation-2
Step 3: comparing equation-1 and equation-2
Now we converted equation-2 in slope intercept form i.e. \[y = mx + c\]
After comparing both equations with each other we get,
 \[m = - 3\]& \[c = 5\]
Hence, slope is equal to \[ - 3\] and intercept on y-axis is equal to \[5\]

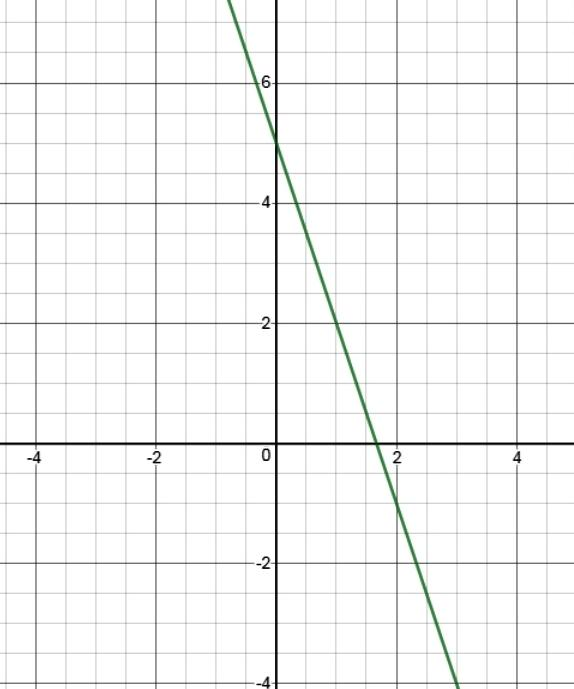
Additional information: We may also have an equation in general form, \[ax + by + c = 0\] which also represents a straight line.
1) Slope of this line = \[ - \dfrac{a}{b}\]\[ = \] \[ - \dfrac{{coeff.of(x)}}{{coeff.of(y)}}\]
2) Intercept by this line on x-axis\[ = - \dfrac{c}{a}\] and intercept by this line on y-axis\[ = - \dfrac{c}{b}\]

Note: Here we should have knowledge of few equations following as:
> Equation of a line parallel to x-axis at a distance \[a\]is \[y = a\]or \[y = - a\]
> Equation of x-axis is \[y = 0\]
> Equation of line parallel to y-axis at a distance \[b\]is \[x = b\]or \[x = - b\]
> Equation of y-axis is \[x = 0\]