
How do you sketch \[y=\sin \left( \dfrac{x}{2} \right)\].?
Answer
524.4k+ views
Hint: We need to graph the given function. We will use the domain and some values of x lying between \[-\pi \] and \[\pi \] to find some values of y. Then, we will use the values of y to find the coordinates of points lying on the required graph, and use the coordinates obtained to graph the function.
Complete step-by-step solution:
The domain of all sine functions is the set of all real numbers.
Thus, the domain of the function \[y=\sin \left( \dfrac{x}{2} \right)\] is given by \[\left\{ x:x\in R \right\}\]. It means that the \[y=\sin \left( \dfrac{x}{2} \right)\] function exists for all x values, and is a continuous function.
Now, we will find some values of y for some values of x lying between \[-\pi \] and \[\pi \].
Substituting \[x=-\pi \] in the function \[y=\sin \left( \dfrac{x}{2} \right)\], we get
\[y=\sin \left( \dfrac{x}{2} \right)\Rightarrow y=\sin \left( -\dfrac{\pi }{2} \right)\]
Simplifying the expression, we get
\[\begin{align}
& y=-\sin \left( \dfrac{\pi }{2} \right) \\
& y=-1 \\
\end{align}\]
Substituting \[x=-\dfrac{3\pi }{4}\] in the function \[y=\sin \left( \dfrac{x}{2} \right)\] , we get
\[\Rightarrow y=\sin \left( \dfrac{-\dfrac{3\pi}{4}}{2} \right)\]
\[\Rightarrow y=\sin \left( \dfrac{-3\pi }{8} \right)\]
As sine function is an odd function, so we can write as
\[y=-\sin \left( \dfrac{3\pi }{8} \right)\]
Substituting the value of the angle, we get
\[y=-1\]
Substituting \[x=-\dfrac{\pi }{2}\] in the function \[y=\sin \left( \dfrac{x}{2} \right)\], we get
\[\Rightarrow y=\sin \left( \dfrac{-\dfrac{\pi }{2}}{2} \right)\]
\[\Rightarrow y=\sin \left( \dfrac{-\pi }{4} \right)\]
As sine function is an odd function, so we can write as
\[\Rightarrow y=-\sin \left( \dfrac{\pi }{4} \right)\]
Substituting the value of the angle, we get
\[y=-\dfrac{1}{\sqrt{2}}\]
Substituting \[x=-\dfrac{\pi }{4}\] in the function \[y=\sin \left( \dfrac{x}{2} \right)\], we get
\[\Rightarrow y=\sin \left( \dfrac{-\dfrac{\pi }{4}}{2} \right)\]
\[\Rightarrow y=\sin \left( -\dfrac{\pi }{8} \right)\]
Substituting the value of the angle, we get
\[y=-0.38269\]
Substituting \[x=0\] in the function \[y=\sin \left( \dfrac{x}{2} \right)\], we get
\[\begin{align}
& \Rightarrow y=\sin \left( \dfrac{0}{2} \right) \\
& \Rightarrow y=\sin \left( 0 \right) \\
\end{align}\]
Substituting the value of the angle, we get
\[y=0\]
Substituting \[x=\dfrac{\pi }{4}\]in the function \[y=\sin \left( \dfrac{x}{2} \right)\], we get
\[\Rightarrow y=\sin \left(\dfrac{ \dfrac{\pi }{4}}{2} \right)\]
\[\Rightarrow y=\sin \dfrac{\pi }{8}\]
Substituting the value of the angle, we get
\[y=0.38269\]
Substituting \[x=\dfrac{\pi }{2}\] in the function \[y=\sin \left( \dfrac{x}{2} \right)\], we get
\[\begin{align}
& \Rightarrow y=\sin \left( \dfrac{\dfrac{\pi }{2}}{2} \right) \\
& \Rightarrow y=\sin \left( \dfrac{\pi }{4} \right) \\
\end{align}\]
Substituting the value of the angle, we get
\[y=\dfrac{1}{\sqrt{2}}\]
Substituting \[x=\dfrac{3\pi }{4}\] in the function \[y=\sin \left( \dfrac{x}{2} \right)\], we get
\[\begin{align}
& \Rightarrow y=\sin \left( \dfrac{\dfrac{3\pi }{4}}{2} \right) \\
& \Rightarrow y=\sin \left( \dfrac{3\pi }{8} \right) \\
\end{align}\]
Substituting the value of the angle, we get
\[y=1\]
Substituting \[x=\pi \] in the function \[y=\sin \left( \dfrac{x}{2} \right)\], we get
\[\Rightarrow y=\sin \left( \dfrac{\pi }{2} \right)\]
Substituting the value of the angle, we get
\[y=1\]
Arranging the values of x and y in a table and writing the coordinates, we get
Now we will use these coordinates of the points to plot the required graph.
Plotting the graphs and joining the curve, we get
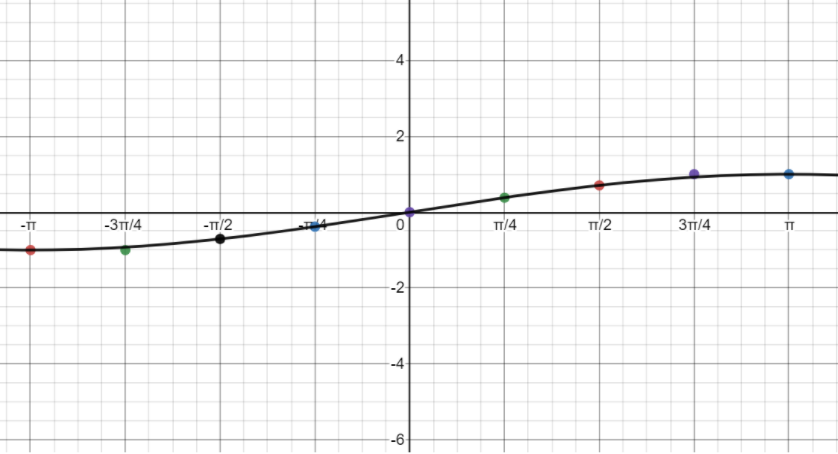
This is the required graph of the function \[y=\sin \left( \dfrac{x}{2} \right)\].
Note: Whenever such types of questions appear, make sure you have drawn the graph correctly. The period of a function \[y=\sin kx\] is given by \[\dfrac{2\pi }{k}\]. The period of the function \[y=\sin \left( \dfrac{x}{2} \right)\] is \[\dfrac{2\pi }{\dfrac{1}{2}}=4\pi \].this means that the graph of \[y=\sin \left( \dfrac{x}{2} \right)\] will repeat for every distance on the x-axis. The range of the sine function is from -1 to 1.
Complete step-by-step solution:
The domain of all sine functions is the set of all real numbers.
Thus, the domain of the function \[y=\sin \left( \dfrac{x}{2} \right)\] is given by \[\left\{ x:x\in R \right\}\]. It means that the \[y=\sin \left( \dfrac{x}{2} \right)\] function exists for all x values, and is a continuous function.
Now, we will find some values of y for some values of x lying between \[-\pi \] and \[\pi \].
Substituting \[x=-\pi \] in the function \[y=\sin \left( \dfrac{x}{2} \right)\], we get
\[y=\sin \left( \dfrac{x}{2} \right)\Rightarrow y=\sin \left( -\dfrac{\pi }{2} \right)\]
Simplifying the expression, we get
\[\begin{align}
& y=-\sin \left( \dfrac{\pi }{2} \right) \\
& y=-1 \\
\end{align}\]
Substituting \[x=-\dfrac{3\pi }{4}\] in the function \[y=\sin \left( \dfrac{x}{2} \right)\] , we get
\[\Rightarrow y=\sin \left( \dfrac{-\dfrac{3\pi}{4}}{2} \right)\]
\[\Rightarrow y=\sin \left( \dfrac{-3\pi }{8} \right)\]
As sine function is an odd function, so we can write as
\[y=-\sin \left( \dfrac{3\pi }{8} \right)\]
Substituting the value of the angle, we get
\[y=-1\]
Substituting \[x=-\dfrac{\pi }{2}\] in the function \[y=\sin \left( \dfrac{x}{2} \right)\], we get
\[\Rightarrow y=\sin \left( \dfrac{-\dfrac{\pi }{2}}{2} \right)\]
\[\Rightarrow y=\sin \left( \dfrac{-\pi }{4} \right)\]
As sine function is an odd function, so we can write as
\[\Rightarrow y=-\sin \left( \dfrac{\pi }{4} \right)\]
Substituting the value of the angle, we get
\[y=-\dfrac{1}{\sqrt{2}}\]
Substituting \[x=-\dfrac{\pi }{4}\] in the function \[y=\sin \left( \dfrac{x}{2} \right)\], we get
\[\Rightarrow y=\sin \left( \dfrac{-\dfrac{\pi }{4}}{2} \right)\]
\[\Rightarrow y=\sin \left( -\dfrac{\pi }{8} \right)\]
Substituting the value of the angle, we get
\[y=-0.38269\]
Substituting \[x=0\] in the function \[y=\sin \left( \dfrac{x}{2} \right)\], we get
\[\begin{align}
& \Rightarrow y=\sin \left( \dfrac{0}{2} \right) \\
& \Rightarrow y=\sin \left( 0 \right) \\
\end{align}\]
Substituting the value of the angle, we get
\[y=0\]
Substituting \[x=\dfrac{\pi }{4}\]in the function \[y=\sin \left( \dfrac{x}{2} \right)\], we get
\[\Rightarrow y=\sin \left(\dfrac{ \dfrac{\pi }{4}}{2} \right)\]
\[\Rightarrow y=\sin \dfrac{\pi }{8}\]
Substituting the value of the angle, we get
\[y=0.38269\]
Substituting \[x=\dfrac{\pi }{2}\] in the function \[y=\sin \left( \dfrac{x}{2} \right)\], we get
\[\begin{align}
& \Rightarrow y=\sin \left( \dfrac{\dfrac{\pi }{2}}{2} \right) \\
& \Rightarrow y=\sin \left( \dfrac{\pi }{4} \right) \\
\end{align}\]
Substituting the value of the angle, we get
\[y=\dfrac{1}{\sqrt{2}}\]
Substituting \[x=\dfrac{3\pi }{4}\] in the function \[y=\sin \left( \dfrac{x}{2} \right)\], we get
\[\begin{align}
& \Rightarrow y=\sin \left( \dfrac{\dfrac{3\pi }{4}}{2} \right) \\
& \Rightarrow y=\sin \left( \dfrac{3\pi }{8} \right) \\
\end{align}\]
Substituting the value of the angle, we get
\[y=1\]
Substituting \[x=\pi \] in the function \[y=\sin \left( \dfrac{x}{2} \right)\], we get
\[\Rightarrow y=\sin \left( \dfrac{\pi }{2} \right)\]
Substituting the value of the angle, we get
\[y=1\]
Arranging the values of x and y in a table and writing the coordinates, we get
| \[x\] | \[y\] | \[\left( x,y \right)\] |
| \[-\pi \] | \[-1\] | \[\left( -\pi ,-1 \right)\] |
| \[-\dfrac{3\pi }{4}\] | \[-1\] | \[\left( -\dfrac{3\pi }{4},-1 \right)\] |
| \[-\dfrac{\pi }{2}\] | \[\dfrac{-1}{\sqrt{2}}\] | \[\left( -\dfrac{\pi }{2},-\dfrac{1}{\sqrt{2}} \right)\] |
| \[-\dfrac{\pi }{4}\] | \[-0.38269\] | \[\left( -\dfrac{\pi }{4},-0.38269 \right)\] |
| \[0\] | \[0\] | \[\left( 0,0 \right)\] |
| \[\dfrac{\pi }{4}\] | \[0.38269\] | \[\left( \dfrac{\pi }{4},0.38269 \right)\] |
| \[\dfrac{\pi }{2}\] | \[\dfrac{1}{\sqrt{2}}\] | \[\left( \dfrac{\pi }{2},\dfrac{1}{\sqrt{2}} \right)\] |
| \[\dfrac{3\pi }{4}\] | \[1\] | \[\left( \dfrac{3\pi }{4},1 \right)\] |
| \[\pi \] | \[1\] | \[\left( \pi ,1 \right)\] |
Now we will use these coordinates of the points to plot the required graph.
Plotting the graphs and joining the curve, we get

This is the required graph of the function \[y=\sin \left( \dfrac{x}{2} \right)\].
Note: Whenever such types of questions appear, make sure you have drawn the graph correctly. The period of a function \[y=\sin kx\] is given by \[\dfrac{2\pi }{k}\]. The period of the function \[y=\sin \left( \dfrac{x}{2} \right)\] is \[\dfrac{2\pi }{\dfrac{1}{2}}=4\pi \].this means that the graph of \[y=\sin \left( \dfrac{x}{2} \right)\] will repeat for every distance on the x-axis. The range of the sine function is from -1 to 1.
Recently Updated Pages
While covering a distance of 30km Ajeet takes 2 ho-class-11-maths-CBSE

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Explain zero factorial class 11 maths CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Why is 1 molar aqueous solution more concentrated than class 11 chemistry CBSE

SiO2GeO2 SnOand PbOare respectively A acidic amphoteric class 11 chemistry CBSE

Fill in the map of Punjab Before 1947 AD i Chamkaur class 11 social science CBSE

How do I convert ms to kmh Give an example class 11 physics CBSE




