
Sketch the graph for $ y = {\tan ^{ - 1}}(\tan x) $
Answer
577.5k+ views
Hint:
To sketch the graph of $ y = {\tan ^{ - 1}}(\tan x) $ . First, we have to calculate the domain and range of tanx and $ {\tan ^{ - 1}} $ . From this, we can sketch the graph of $ \tan x $ and $ {\tan ^{ - 1}} $ . With the help of these, we can draw a graph of $ y = {\tan ^{ - 1}}(\tan x) $
In a relation R from set A to set B, the set of all first components of order pair belongings to R is called the domain and all the second element of pair is called range.
Complete step by step solution:
We know that the domain of tan. function(tangent function) is the set $ \left\{ {x:x \in R,and.x \ne (2n + 1)\dfrac{\pi }{2},n \in Z} \right\} $
here R represents the real number and $ x \ne (2n + 1)\dfrac{\pi }{2} $ means the domain of tan function does not contain an odd multiple of $ \dfrac{\pi }{2} $ . $ n \in Z $ Represents that n is an integer. Z is the symbol of an integer.
The range of the tan function in R. Here R represents the real number. If we restrict the domain of a tangent function to $ \left( {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right) $ then it is one-one and onto with the range R. So, the tangent function is restricted to any of interval etc, is bijective and range is R. SO, $ {\tan ^{ - 1}} $ can be defined as the function whose domain is R and range could be any of interval $ \left( {\dfrac{{ - 3\pi }}{2},\dfrac{\pi }{2}} \right),\left( {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right),\left( {\dfrac{\pi }{2},\dfrac{{3\pi }}{2}} \right) $ and so on. This interval gives different branches of the function $ {\tan ^{ - 1}} $ . The branch $ \left( {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right) $ is called the principal value branch of the function $ {\tan ^{ - 1}} $ therefor $ {\tan ^{ - 1}}:R \to \left( {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right) $
The graph of a tan function $ y = \tan x $ is given as:
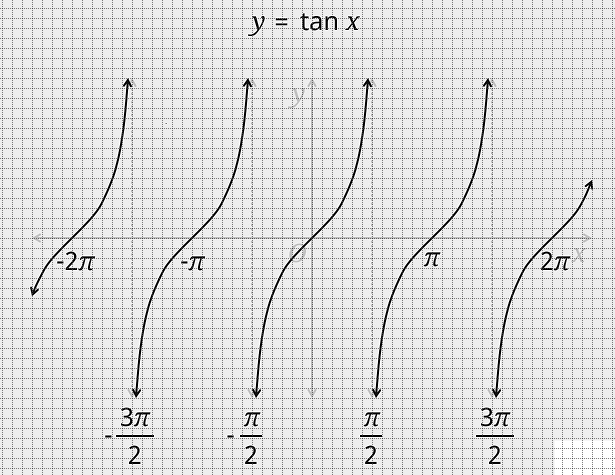
The graph of $ y = {\tan ^{ - 1}}x $ is given as
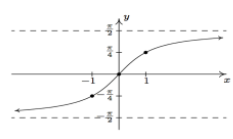
As $ y = {\tan ^{ - 1}}(\tan x) $ is periodic with period π. therefore to draw this graph we should draw the graph for one interval $ \pi $ and repeat for the entire value.
As we know that $ y = {\tan ^{ - 1}}(\tan x) $ = $ \left\{ {x:\dfrac{\pi }{2} < x < \dfrac{\pi }{2}} \right\} $
This has been defined for $ \dfrac{\pi }{2} < x < \dfrac{\pi }{2} $ that has a length $ \pi $ so its graph could be plotted as
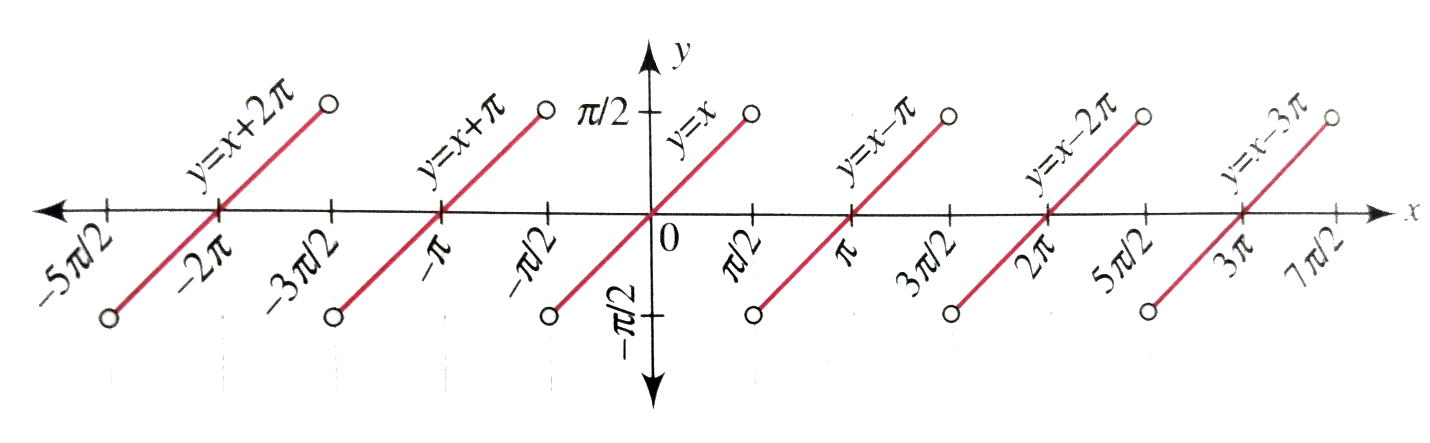
Thus this graph of y where y is not defined for $ x \in (2n + 1)\dfrac{\pi }{2} $ .
Note:
One-one function: A function $ f:x \to y $ is defined as a one-one function of the image of distinct elements of X under $ f $ are distinct.
Onto function: A function is $ f:x \to y $ said to be onto the function of every element of Y is an image of some element of X under f.
Bijective Function: The function which is both one-one and onto is called the bijective function.
To sketch the graph of $ y = {\tan ^{ - 1}}(\tan x) $ . First, we have to calculate the domain and range of tanx and $ {\tan ^{ - 1}} $ . From this, we can sketch the graph of $ \tan x $ and $ {\tan ^{ - 1}} $ . With the help of these, we can draw a graph of $ y = {\tan ^{ - 1}}(\tan x) $
In a relation R from set A to set B, the set of all first components of order pair belongings to R is called the domain and all the second element of pair is called range.
Complete step by step solution:
We know that the domain of tan. function(tangent function) is the set $ \left\{ {x:x \in R,and.x \ne (2n + 1)\dfrac{\pi }{2},n \in Z} \right\} $
here R represents the real number and $ x \ne (2n + 1)\dfrac{\pi }{2} $ means the domain of tan function does not contain an odd multiple of $ \dfrac{\pi }{2} $ . $ n \in Z $ Represents that n is an integer. Z is the symbol of an integer.
The range of the tan function in R. Here R represents the real number. If we restrict the domain of a tangent function to $ \left( {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right) $ then it is one-one and onto with the range R. So, the tangent function is restricted to any of interval etc, is bijective and range is R. SO, $ {\tan ^{ - 1}} $ can be defined as the function whose domain is R and range could be any of interval $ \left( {\dfrac{{ - 3\pi }}{2},\dfrac{\pi }{2}} \right),\left( {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right),\left( {\dfrac{\pi }{2},\dfrac{{3\pi }}{2}} \right) $ and so on. This interval gives different branches of the function $ {\tan ^{ - 1}} $ . The branch $ \left( {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right) $ is called the principal value branch of the function $ {\tan ^{ - 1}} $ therefor $ {\tan ^{ - 1}}:R \to \left( {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right) $
The graph of a tan function $ y = \tan x $ is given as:
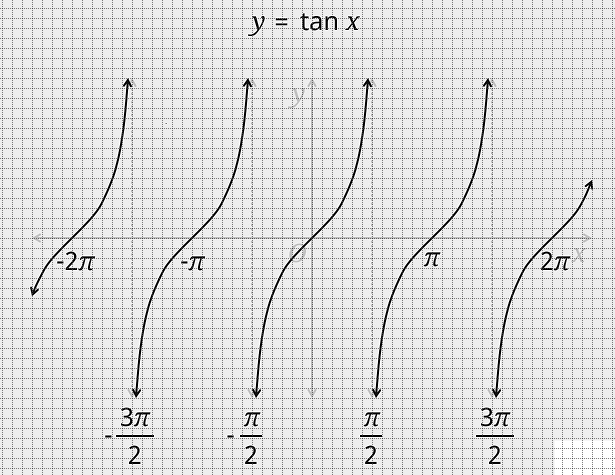
The graph of $ y = {\tan ^{ - 1}}x $ is given as

As $ y = {\tan ^{ - 1}}(\tan x) $ is periodic with period π. therefore to draw this graph we should draw the graph for one interval $ \pi $ and repeat for the entire value.
As we know that $ y = {\tan ^{ - 1}}(\tan x) $ = $ \left\{ {x:\dfrac{\pi }{2} < x < \dfrac{\pi }{2}} \right\} $
This has been defined for $ \dfrac{\pi }{2} < x < \dfrac{\pi }{2} $ that has a length $ \pi $ so its graph could be plotted as

Thus this graph of y where y is not defined for $ x \in (2n + 1)\dfrac{\pi }{2} $ .
Note:
One-one function: A function $ f:x \to y $ is defined as a one-one function of the image of distinct elements of X under $ f $ are distinct.
Onto function: A function is $ f:x \to y $ said to be onto the function of every element of Y is an image of some element of X under f.
Bijective Function: The function which is both one-one and onto is called the bijective function.
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Explain zero factorial class 11 maths CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Chemical formula of Bleaching powder is A Ca2OCl2 B class 11 chemistry CBSE

Draw a diagram of nephron and explain its structur class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

A solution of a substance X is used for white washing class 11 chemistry CBSE




